Real time optimization of sensor data to reduce log file size by omiting entries

Question

Updated several times to better describe the current implementation and its usage which was lacking.

What I want to do: I would like to log real time sensor(s) data (voltage) to a log file (CSV) in a size efficient manner (least number of rows). Each row must contain all the sensor data at a specific timestamp. This should allow easy graphing, with X-axis being time.

Currently a new row is added every second with all the sensor data.

A typical problem is that the sensor data does not change for days (similar voltage) but then suddenly changes (large voltage change) every few seconds for a short period of time.

In this case I would like to optimize the log file to only include few points when the data is not changing much, but still capture the period of fast changes.

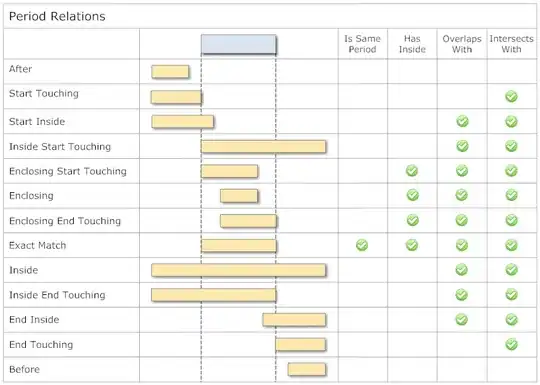
For example, in the following set of data and I only want a new point when the data changes by more than 10.

+-----------------------------+
|  Time(sec) Value1   Value2  |
+-----------------------------+
| 1           0        0      |
| 2           5        3      |
| 3           0        1      |
| ...thousand entries...      |
| 1001        15       1      |
| 1002        12       4      |
| 1003        2        1      |
| 1004        3        2      |
|         ...............     |
+-----------------------------+

Ideally the output would be:

+-----------------------------+
|  Time(sec) Value1   Value2  |
+-----------------------------+
| 1           0        0      |
| 1000        5        3      | <<last value? Mean? extrapolation?
| 1001        15       1      |
| 1002        12       4      | <<last value? Mean? extrapolation?
| 1003        2        1      |
|         ...............     |
+-----------------------------+

The algorithm must handle large sudden value changes with out the resultant looking like a gradual increase, this would happen if in the above example only points 1,1001,1003 where included in the output. It would look like a pyramid rather than a step change!

They are also details such as in the above output example, point 1000, should it be the last point before the step change, or a mean value between all the points from 1-1000?

Ideally an algorithm exist where the optimized output represents the input waveform as accurately as possible.

Current Implementation

Currently all the sensor data is saved once a second to a CSV file. It is then used by non-technical people to view the the trend inside excel or similar by plotting a graph.

The files generated are often very large.

Research

I had a look at Online Linear Regression but I dont think what I want to achieve is curve fitting.

Essentially I dont know what keyword to search for to describe this problem. I have tried the following:

• "how to optimize data captured in a csv file"
• "real time data optimisation by data change algorithm"
• "real time data optimisation by point removal"

Run-length encoding or other encoding pattern compression would no longer allow the user to open the output file for easy graphing. It would first have to be decoded.

"Online Algorithm" Is the name for the general class of algorithms which process input in a serial fashion

Questions:

The resulting CSV file must still be human readable and easily graph-able in excel or similar. This rules out compression or encoding the number of entries in the CSV file.

1. Is their a name for this class of problems / algorithm?
2. Any commonly used algorithms? (I am programming in C#)

Update 1

An alternative description of what i am looking to happen:

1. A new measurement is taken once a second
2. The algorithm receives each measurement at a time
3. The algorithm output must select/generate the smallest number of points which would represent the original waveform if each point where connected by a line.
4. The algorithm must generate this output "online". It does not have the complete dataset.

This description better captures that the output must be a set of points representing the original waveform.

The output must look like the input waveform once graphed in excel or similar. These tools generally just linearly connect the dots.

Here are two example of what the algorithm should be doing. The input data is simplified to be represented with many less points. (Note: Y scales are not identical between examples, the optimization strength would be user controllable)

Update 2 Looks like what I am looking may be related to: "Online piecewise linear interpolation"

I have found "piecewise linear interpolation" trying to see if they work for streaming data.

Update 3 "piecewise linear interpolation" is not quite the right algorithm either. This would linearly interpolate between existing points, while i want to generate a new set of points to represent the original data..

Maybe keep monitor the incoming data since the last knot and once all the data can no longer be represented by a line, insert a new knot and restart? Obvious issue is how to optimally choose where to put the knot..

Final Update Added my own answer below. Algorithms called "Line Simplification algorithms" or "downsampling"/ "data compression" algorithms. The "downsampling"/ "data compression" appears better geared to streaming data.

Will most likely use the "Fan" data compression Algorithms for my problem.

Answer 1

If the voltage doesn't change at all for long periods, all you need is run-length encoding, which can be trivially done on the fly by comparing the value you are about to save with the last value you saved.

If you want to ignore voltage changes that are less than some small specified amount, then you can simply change the above equality comparison to a test of the magnitude of the difference: is |curValue - lastWrittenValue| > threshold? -- and use RLE as before.

Answer 2

The algorithm category could be "Line Simplification algorithms" or "downsampling"/ "data compression" algorithms:

Line Simplification algorithms

An example would be the "Ramer–Douglas–Peucker algorithm" / "iterative end-point fit algorithm" and "split-and-merge algorithm".

A C# implemententation:A-Csharp-Implementation-of-Douglas-Peucker-Line-Ap.

Some can be used for streaming data, such as Streaming Algorithms for Line Simplification.

History of research here: Curve Simplification Turk

Downsampling/ "data compression" algorithms

Question already answered here: downsampling-excessively-sampled-curves

Answer 3

Not sure if there is a common name for this. You can save this in the following format

+------------------------+
|   from   to   value    |
+------------------------+
| time1  time 2  123.345 |
| time2  time 3  13.5    |
| time4  time 5  128.2   |
+------------------------+

Save the value only when it deviates significantly from the previous value. The algorithm:

• Loop
• Remember: start_time, start_value
• Get current_value and compare against start_value
  • No difference => keep going
  • Significantly different => write to csv (start_time, end_time, start_value)

Answer 4

Something very simple you could do is to use a windowed running average and standard deviation, with a specific window size that spans a modest time period (e.g. 30-40 seconds @ a sampling rate of 1 observation per second) and a specific confidence limit that you want to use to detect deviations (e.g. +/- 2 SD). This will cover a certain period of the most recent observations only, and will allow you to determine if a newly arrived sensor observation deviates from them.

Then, if a newly arrived observation

• Falls outside the confidence limit → log it to your csv & clear the window.
• Falls inside the confidence limit → don't log it to your csv file.

As long as the window is not filled with observations (i.e. it is stabilizing) you also log new observations.

If you combine this with a second avg/sd window that periodically receives the average for the recent period, you can also detect trends over a somewhat larger period.

Note that an added advantage is, that you also have standard deviations available for the voltage observations, if at some point in the future you would like to do more than just monitor individual values.

An implementation of a running average/SD calculator can be found here https://stackoverflow.com/a/29269137/2573395. For this problem, I adapted it a bit to also keep track of the time stamps and allow checking if an observation falls in the confidence interval.

public class MovingAverageCalculator
{
    public MovingAverageCalculator(int period)
    {
        _period = period;
        _window = new double[period];
        _stamps = new DateTime[period];
    }

    public double Average
    {
        get { return _average; }
    }

    public double StandardDeviation
    {
        get
        {
            var variance = Variance;
            if (variance >= double.Epsilon)
            {
                var sd = Math.Sqrt(variance);
                return double.IsNaN(sd) ? 0.0 : sd;
            }
            return 0.0;
        }
    }

    public double Variance
    {
        get
        {
            var n = N;
            return n > 1 ? _variance_sum / (n - 1) : 0.0;
        }
    }

    public bool HasFullPeriod
    {
        get { return _num_added >= _period; }
    }

    public IEnumerable<double> Observations
    {
        get { return _window.Take(N); }
    }

    public IEnumerable<DateTime> TimeStamps
    {
        get { return _stamps.Take(N); }
    }

    public int N
    {
        get { return Math.Min(_num_added, _period); }
    }

    public int WindowSize
    {
        get { return _window.Length; }
    }

    public bool IsOutOfBounds(double observation, double maxSDDeviation)
    {
        var dev = maxSDDeviation * StandardDeviation;
        return observation < _average - dev || observation > _average + dev;
    }

    public void Clear()
    {
        _num_added = 0;
        _average = 0;
        _variance_sum = 0;
    }

    public void AddObservation(DateTime stamp, double observation)
    {
        // Window is treated as a circular buffer.
        var ndx = _num_added % _period;
        var old = _window[ndx];     // get value to remove from window
        _window[ndx] = observation; // add new observation in its place.
        _stamps[ndx] = stamp;
        _num_added++;

        // Update average and standard deviation using deltas
        var old_avg = _average;
        if (_num_added <= _period)
        {
            var delta = observation - old_avg;
            _average += delta / _num_added;
            _variance_sum += (delta * (observation - _average));
        }
        else // use delta vs removed observation.
        {
            var delta = observation - old;
            _average += delta / _period;
            _variance_sum += (delta * ((observation - _average) + (old - old_avg)));
        }
    }

    private readonly int _period;
    private double[] _window;
    private DateTime[] _stamps;
    private int _num_added;
    private double _average;
    private double _variance_sum;
}

The below class provides an example implementation that uses the mentioned strategy using two "chained" moving avg/sd windows.

public class VoltageObservationFilter
{
    private readonly MovingAverageCalculator _shortPeriodCalculator;
    private readonly MovingAverageCalculator _longPeriodCalculator;
    private readonly Action<ObservationType, DateTime, double> _onFilteredObservation;
    private readonly double _maxSDDeviation;
    private int _periodCounter;

    public enum ObservationType
    {
        kNewObservation,
        kRecentPeriodAverage,
        kLongPeriodAverage
    };

    public VoltageObservationFilter(
        Action<ObservationType, DateTime, double> onFilteredObservation,
        double maxSDDeviation,
        TimeSpan samplingInterval,
        TimeSpan shortPeriod,
        TimeSpan longPeriod)
    {
        var shortWindowSize = (int)Math.Round(shortPeriod.TotalMilliseconds / samplingInterval.TotalMilliseconds);
        var longWindowSize = (int)Math.Round(longPeriod.TotalMilliseconds / shortPeriod.TotalMilliseconds);
        _shortPeriodCalculator = new MovingAverageCalculator(shortWindowSize);
        _longPeriodCalculator = new MovingAverageCalculator(longWindowSize);
        _onFilteredObservation = onFilteredObservation;
        _maxSDDeviation = maxSDDeviation;
    }

    public void AddObservation(DateTime timeStamp, double voltage)
    {
        if (DoAddObservation(_shortPeriodCalculator, timeStamp, voltage))
        {
            _onFilteredObservation(ObservationType.kNewObservation, timeStamp, voltage);
            _periodCounter = _shortPeriodCalculator.N;
        }
        else if (_periodCounter++ == _shortPeriodCalculator.WindowSize)
        {
            // chaining: add short period average to long period.
            _periodCounter = 0;
            var avgObs = _shortPeriodCalculator.Average;
            var avgTicks = _shortPeriodCalculator.TimeStamps.Average(ts => ts.Ticks);
            var avgStamp = new DateTime((long)Math.Round(avgTicks));
            if (DoAddObservation(_longPeriodCalculator, avgStamp, avgObs))
            {
                _onFilteredObservation(ObservationType.kRecentPeriodAverage, avgStamp, avgObs);
                avgObs = _longPeriodCalculator.Average;
                avgTicks = _longPeriodCalculator.TimeStamps.Average(ts => ts.Ticks);
                avgStamp = new DateTime((long)Math.Round(avgTicks));
                _onFilteredObservation(ObservationType.kLongPeriodAverage, avgStamp, avgObs);
            }
        }
    }

    private bool DoAddObservation(MovingAverageCalculator calculator, DateTime timeStamp, double observation)
    {
        if (!calculator.HasFullPeriod)
        {
            calculator.AddObservation(timeStamp, observation);
            return true; // still stabilizing: log 
        }
        else if (calculator.IsOutOfBounds(observation, _maxSDDeviation))
        {
            calculator.Clear(); // deviation: reset window.
            return true; // requires logging
        }
        else
        {
            calculator.AddObservation(timeStamp, observation);
            return false; // falls within bounds, no logging.
        }
    }
}