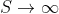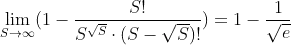What are the chances of a collision?
The exact probability that n hashes collide with S the total number of different possible hashes is:

(perfect behaviour of hash function, birthday paradox, blah blah blah...)
You wont be able to compute this directly, since those are huge numbers, so we use limits and make 2 assumptions:
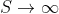
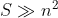
With those 2 assumptions, the probability of a collision can be computed with:

Now you can compute the probability of a collision for some number n of records. This is very very accurate for anything less than 2^70 records for sha1 (S=2^160), the worse the approximation the more n approach 2^80.
Example
For example if you want to save a huge number of users, specifically the same number as person are in the world (~ 8 billions), and you are using sha1 (S=2^160), the probability of a collision is 2.5e-29 (notice that the 2 assumptions hold). To give you a reference, the probability of wining the Euromillion Jackpot is 7e-9 approx.
Curiosity: What to do with larger (larger?!) numbers?
Compute directly the limit without the second assumption.
For example, the first collision is expected around the square root of S, (in the case of sha1 n=2^80). At that value, the second condition doesn't hold but we can compute the limit directly with:
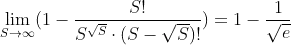
which is a 40% approx. of probability of a collision.