This great SO answer points to a good sparse solver for Ax=b, but I've got constraints on x such that each element in x is >=0 an <=N.
Also, A is huge (around 2e6x2e6) but very sparse with <=4 elements per row.
Any ideas/recommendations? I'm looking for something like MATLAB's lsqlin but with huge sparse matrices.
I'm essentially trying to solve the large scale bounded variable least squares problem on sparse matrices:
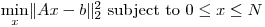
EDIT: In CVX:
cvx_begin
variable x(n)
minimize( norm(A*x-b) );
subject to
x <= N;
x >= 0;
cvx_end


