4

Many random-number generators return floating numbers between 0 and 1.

What's the best and correct way to get integers between a and b?

skaffman
  • 398,947
  • 96
  • 818
  • 769
Georg Schölly
  • 124,188
  • 49
  • 220
  • 267
  • 1
    Do you want `b` to be as improbable as `1.0` in a "normal" (`[0,1]`) random number? Or should all integer numbers in this range have the same probability? – Tim Pietzcker Jun 14 '10 at 09:56
  • @Tim: All integer numbers should hav ethe same probability. (That's what makes it harder.) – Georg Schölly Jun 14 '10 at 11:26
  • If (B-A) = n, you should map n+1 intervals (bins) in [0,1] to integers in [A,B] The way to construct the intervals is by taking (n) divisions of the interval [0,1] (one division i.e in 0.5 map to two consecutive integers A,A+1). If the random number lies in interval (i) the corresponding integer is A+i-1. – Dr. belisarius Jun 14 '10 at 11:36

5 Answers5

6

Divide the interval [0,1] in B-A+1 bins

Example A=2, B=5

        [----+----+----+----]
        0    1/4  1/2  3/4  1
Maps to    2    3    4    5

The problem with the formula

 Int (Rnd() * (B-A+1)) + A

is that your Rnd() generation interval is closed on both sides, thus the 0 and the 1 are both possible outputs and the formula gives 6 when the Rnd() is exactly 1.

In a real random distribution (not pseudo), the 1 has probability zero. I think it is safe enough to program something like:

 r=Rnd()
 if r equal 1
     MyInt = B
 else
     MyInt = Int(r * (B-A+1)) + A
 endif

Edit

Just a quick test in Mathematica:

Define our function:

f[a_, b_] :=  If[(r = RandomReal[]) == 1, b, IntegerPart[r (b - a + 1)] + a]

Build a table with 3 10^5 numbers in [1,100]: 

table = SortBy[Tally[Table[f[1, 100], {300000}]], First]

Check minimum and maximum: 

In[137]:= {Max[First /@ table], Min[First /@ table]}

Out[137]= {100, 1}

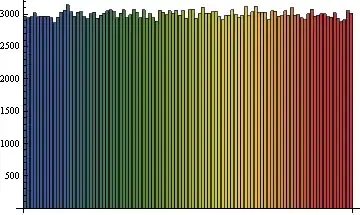
Lets see the distribution: 

BarChart[Last /@ SortBy[Tally[Table[f[1, 100], {300000}]], First],
        ChartStyle -> "DarkRainbow"]

alt text

Dr. belisarius
  • 60,527
  • 15
  • 115
  • 190
  • Or if you prefer, mapping the 6 to 2 instead of to 5 // mod(Int(r*(B-A+1), (B-A+1)))+A – Dr. belisarius Jun 14 '10 at 12:40
  • In Python, `random.random()` returns a value between 0 and "just below" 1, so also the pseudo-random number is safe. See http://stackoverflow.com/questions/3037952 – Tim Pietzcker Jun 14 '10 at 14:35
  • @Tim Pietzcker That's good! (although implementation dependent) – Dr. belisarius Jun 14 '10 at 15:27
  • @user359996 The question is tagged as "language-agnostic", so I tried to give a general answer. I believe the algorithm works irrespective to the openness of the source interval. The usual notation in mathematics is to use "[..]" for closed intervals and "(..)" for open ones. And the OP uses "[..]" – Dr. belisarius Jun 28 '10 at 21:03
1
X = (Rand() * (B - A)) + A
nothrow
  • 15,882
  • 9
  • 57
  • 104
1

Another way to look at it, where r is your random number in the range 0 to 1:

(1-r)a + rb

As for your additional requirement of the result being an integer, maybe (apart from using built in casting) the modulus operator can help you out. Check out this question and the answer:

Expand a random range from 1–5 to 1–7

Community
  • 1
  • 1
zaf
  • 22,776
  • 12
  • 65
  • 95
  • I don't think the linked question is of use here, since in that question the generated random number is an integer value. – Joachim Sauer Jun 14 '10 at 10:00
  • In the question, whats that word in bold? – zaf Jun 14 '10 at 10:02
  • I think Joachim Sauer is referring to the input, not the output. In the linked question, a function that returns a random integer between 1 and 5 is transformed into a function that returns an integer between 1 and 7. Those problems are not equivalent. – Tim Pietzcker Jun 14 '10 at 11:06
  • @Tim - Yes. I probably shouldn't have linked that question but I'll leave it there. It may give someone an idea. – zaf Jun 14 '10 at 12:52
1

Well, why not just look at how Python does it itself? Read random.py in your installation's lib directory.

After gutting it to only support the behavior of random.randint() (which is what you want) and removing all error checks for non-integer or out-of-bounds arguments, you get:

import random
def randint(start, stop):
    width = stop+1 - start
    return start + int(random.random()*width)

Testing:

>>> l = []
>>> for i in range(2000000):
...     l.append(randint(3,6))
...
>>> l.count(3)
499593
>>> l.count(4)
499359
>>> l.count(5)
501432
>>> l.count(6)
499616
>>>
Tim Pietzcker
  • 328,213
  • 58
  • 503
  • 561
0

Assuming r_a_b is the desired random number between a and b and r_0_1 is a random number between 0 and 1 the following should work just fine:

r_a_b = (r_0_1 * (b-a)) + a
Joachim Sauer
  • 302,674
  • 57
  • 556
  • 614