How to choose control point distance for 3D cubic Bézier curves to optimize 'roundness'?

Question

Say I want to construct a 3D cubic Bézier curve, and I already have both end-points, and the direction (normal vector) for both control points. How can I choose the distance of both control points to their respective end-points in order to make the curve as 'nicely rounded' as possible?

To formalize 'nicely rounded': I think that means maximizing the smallest angle between any two segments in the curve. For example, having end-points (10, 0, 0) and (0, 10, 0) with respective normal vectors (0, 1, 0) and (1, 0, 0) should result in a 90° circular arc. For the specific case of 2D circular arcs, I've found articles like this one. But I haven't been able to find anything for my more general case.

       

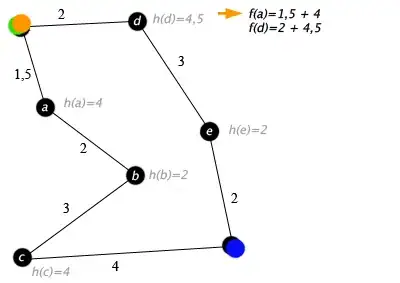
(Note that these images are just to illustrate the 'roundness' concept. My curves are not guaranteed to be plane-aligned. I may replace the images later to better illustrate that point.)

This is a question of aesthetics, and if the real solution is unknown or too complicated, I would be happy with a reasonable approximation. My current approximation is too simplistic: choosing half the distance between the two end-points for both control point distances. Someone more familiar with the math will probably be able to come up with something better.

(PS: This is for open-source software, and I would be happy to give credit on GitHub.)

Edit: Here are some other images to illustrate a 3D case (jsfiddle):

   

Edit 2: Here's a screenshot of an unstable version of ApiNATOMY to give you an idea of what I'm trying to do. I'm creating 3D tubes to represent blood-vessels, connecting different parts of an anatomical schematic:

(They won't let me put in a jsfiddle link if I don't include code...)

Answer 1

What you are basically asking is to have curvature over the spline as constant as possible.

A curve with constant curvature is just a circular arc, so it makes sense to try to fit such an arc to your input parameters. In 2D, this is easy: construct the line which goes through your starting point and is orthogonal to the desired direction vector. Do the same for the ending point. Now intersect these two lines: the result is the center of the circle which passes through the two points with the desired direction vectors.

In your example, this intersection point would just be (0,0), and the desired circular arc lies on the unit circle.

So this gives you a circular arc, which you can either use directly or use the approximation algorithm which you have already cited.

This breaks down when the two direction vectors are collinear, so you'd have to fudge it a bit if this ever comes up. If they point at each other, you can simply use a straight line.

In 3D, the same construction gives you two planes passing through the end points. Intersect these, and you get a line; on this line, choose the point which minimizes the sum of squared distances to the two points. This gives you the center of a sphere which touches both end points, and now you can simply work in the plane spanned by these three points and proceed as in 2D.

Answer 2

For the special case where your two end points and the two known normal vector for the control points happen to make the Bezier curve a planar one, then basically you are looking for a cubic Bezier curve that can well approximate a circular arc. For this special case, you can set the distance (denoted as L) between the control point and their respective end point as L = (4/3)*tan(A/4) where A is the angle of the circular arc.

For the general 3D case, perhaps you can apply the same formula as:

• compute the angle between the two normal vectors.
• use L=(4/3)*tan(A/4) to decide the location of your control points.

Answer 3

if your normals are aligned in a plane

What you're basically doing here is creating an elliptical arc, in 3D, where the "it's in 3D" part is completely irrelevant, since it's just a 2D curve, rotated/translated to sit in your 3D space. So let's just solve the 2D case, and then the RT is entirely up to you.

Creating the "perfect" cubic Bezier between two points on an arc comes with limitations. You basically can't create good looking arcs that span more than a quarter circle. So, with that said: your start and end point normals give you a 2D angle between your normal vectors, which is the same angle as between your start and end tangents (since normals are perpendicular to tangents). So, let's:

1. align our curve so that the tangent at the start is 0
2. plug the angle between tangents into the formula given in the section on Circle approximation in the Primer on Bezier curves. This is basically just dumb "implementing the formula for c1x/c1y/c2x/c2y as a function that takes an angle as argument, and spits out four values as c1(x,y) and c2(x,y) coordinats".
3. There is no step 3, we're done.

After step 2, you have your control points in 2D to create the most circular arc between a start and end point. Now you just need to scale/rotate/translate it in 3D so that it lines up with where you needed your start and end point to begin with.

if your normals are not aligned in a plane

Now we have a problem, although one that we can deal with by treating the dimensions as separate things entirely. Instead of creating a single 2D curve, we're going to create three: one that's the X/Y projection, one that's the X/Z projection, and one that's the Y/Z projection. For all three of these, we're going to abstract the control points in exactly the same way as before, and then we simply take the projective control points (three for each control point), and then go "okay, we now have X, Y, and Z projective coordinates. That means we have (X,Y,Z) coordinates", and done again.