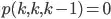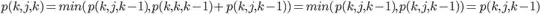why does floyd warshall just use one distance matrix?

Question

I read the pseudocode of the floyd warshall algorithm 1 let dist be a |V| × |V| array of minimum distances initialized to ∞ (infinity) 2 for each vertex v 3 dist[v][v] ← 0 4 for each edge (u,v) 5 dist[u][v] ← w(u,v) // the weight of the edge (u,v) 6 for k from 1 to |V| 7 for i from 1 to |V| 8 for j from 1 to |V| 9 if dist[i][j] > dist[i][k] + dist[k][j] 10 dist[i][j] ← dist[i][k] + dist[k][j] 11 end if But it just uses one dist matrix to save distances. I think there should be n dist matrixes, where n is the number of vertexes, Or at least we need two dist matrixes. one stores the current shortest path within vertexes k-1, the other stores the shortest path within vertexes k, then the first one stores shortest path within k+1, .... How can we just store the new shortest path distances within vertexes k in original matrix for distances within vertexes k-1?

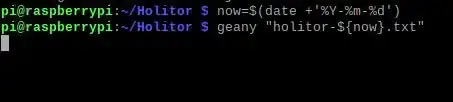
this picture shows we need D0, D1, D2....D(n)

Answer 1

You're right in the sense that the original formula requires that calculations for step k needs to use calculations from step k-1:

That can be organized easily if, as you say, first matrix is used to store values from step k-1 second is used to store values from k, the first one is used again to store values from k+1 etc.

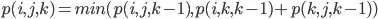
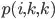But, if we use the same matrix when updating values, in the above formula we might accidentally use instead of 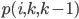if value for index 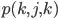i,k has alre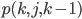ady been updated during the current round k, or we might get instead of if value for index k,j has been updated. Won't that be a violation of the algorithm, as we are using the wrong recursive update formula?

Well, not really. Remember, Floyd-Warshall algorithm deals with "no negative cycles" constraint, which means that there is no cycle with edges that sum to a negative value. This means that for any k the shortest path from node k to node k is 0 (otherwise it would mean that there is a path from k to k with edges that sum to a negative value). So by definition:

Now, let's just take the first formula and replace j with k:

And then let's replace in the same formula 'i' with 'k':

So, basically, will have the same value as and will have the same value as , so it doesn't really matter whether these values are updated or not during the cycle 'k' and so you can update the same matrix while reading it without breaking the algorithm.

Answer 2

You are partially correct here.

The output of Floyd Warshall Algorithm(i.e the NxN matrix) DOESN'T help to reconstruct the actual shortest path between any two given vertices.

These paths can be recovered if we retain a parent matrix P, such that it stores the last intermediate vertex used for each vertex pair (x, y). Say this value is k.

The shortest path from x to y is the concatenation of the shortest path from x to k with the shortest path from k to y, which can be reconstructed recursively given the matrix P.

Note,however, that most all-pairs applications need only the resulting distance matrix.These jobs are what Floyd’s algorithm was designed for.