OpenCV 3.0: Calibration not fitting as expected

Question

I'm getting results I don't expect when I use OpenCV 3.0 calibrateCamera. Here is my algorithm:

1. Load in 30 image points
2. Load in 30 corresponding world points (coplanar in this case)
3. Use points to calibrate the camera, just for un-distorting
4. Un-distort the image points, but don't use the intrinsics (coplanar world points, so intrinsics are dodgy)
5. Use the undistorted points to find a homography, transforming to world points (can do this because they are all coplanar)
6. Use the homography and perspective transform to map the undistorted points to the world space
7. Compare the original world points to the mapped points

The points I have are noisy and only a small section of the image. There are 30 coplanar points from a single view so I can't get camera intrinsics, but should be able to get distortion coefficients and a homography to create a fronto-parallel view.

As expected, the error varies depending on the calibration flags. However, it varies opposite to what I expected. If I allow all variables to adjust, I would expect error to come down. I am not saying I expect a better model; I actually expect over-fitting, but that should still reduce error. What I see though is that the fewer variables I use, the lower my error. The best result is with a straight homography.

I have two suspected causes, but they seem unlikely and I'd like to hear an unadulterated answer before I air them. I have pulled out the code to just do what I'm talking about. It's a bit long, but it includes loading the points.

The code doesn't appear to have bugs; I've used "better" points and it works perfectly. I want to emphasize that the solution here can't be to use better points or perform a better calibration; the whole point of the exercise is to see how the various calibration models respond to different qualities of calibration data.

Any ideas?

Added

To be clear, I know the results will be bad and I expect that. I also understand that I may learn bad distortion parameters which leads to worse results when testing points that have not been used to train the model. What I don't understand is how the distortion model has more error when using the training set as the test set. That is, if the cv::calibrateCamera is supposed to choose parameters to reduce error over the training set of points provided, yet it is producing more error than if it had just selected 0s for K!, K2, ... K6, P1, P2. Bad data or not, it should at least do better on the training set. Before I can say the data is not appropriate for this model, I have to be sure I'm doing the best I can with the data available, and I can't say that at this stage.

Here an example image

The points with the green pins are marked. This is obviously just a test image.

Here is more example stuff

In the following the image is cropped from the big one above. The centre has not changed. This is what happens when I undistort with just the points marked manually from the green pins and allowing K1 (only K1) to vary from 0:

Before

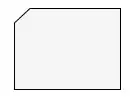
After

I would put it down to a bug, but when I use a larger set of points that covers more of the screen, even from a single plane, it works reasonably well. This looks terrible. However, the error is not nearly as bad as you might think from looking at the picture.

// Load image points
    std::vector<cv::Point2f> im_points;
    im_points.push_back(cv::Point2f(1206, 1454));
    im_points.push_back(cv::Point2f(1245, 1443));
    im_points.push_back(cv::Point2f(1284, 1429));
    im_points.push_back(cv::Point2f(1315, 1456));
    im_points.push_back(cv::Point2f(1352, 1443));
    im_points.push_back(cv::Point2f(1383, 1431));
    im_points.push_back(cv::Point2f(1431, 1458));
    im_points.push_back(cv::Point2f(1463, 1445));
    im_points.push_back(cv::Point2f(1489, 1432));
    im_points.push_back(cv::Point2f(1550, 1461));
    im_points.push_back(cv::Point2f(1574, 1447));
    im_points.push_back(cv::Point2f(1597, 1434));
    im_points.push_back(cv::Point2f(1673, 1463));
    im_points.push_back(cv::Point2f(1691, 1449));
    im_points.push_back(cv::Point2f(1708, 1436));
    im_points.push_back(cv::Point2f(1798, 1464));
    im_points.push_back(cv::Point2f(1809, 1451));
    im_points.push_back(cv::Point2f(1819, 1438));
    im_points.push_back(cv::Point2f(1925, 1467));
    im_points.push_back(cv::Point2f(1929, 1454));
    im_points.push_back(cv::Point2f(1935, 1440));
    im_points.push_back(cv::Point2f(2054, 1470));
    im_points.push_back(cv::Point2f(2052, 1456));
    im_points.push_back(cv::Point2f(2051, 1443));
    im_points.push_back(cv::Point2f(2182, 1474));
    im_points.push_back(cv::Point2f(2171, 1459));
    im_points.push_back(cv::Point2f(2164, 1446));
    im_points.push_back(cv::Point2f(2306, 1474));
    im_points.push_back(cv::Point2f(2292, 1462));
    im_points.push_back(cv::Point2f(2278, 1449));

    // Create corresponding world / object points
    std::vector<cv::Point3f> world_points;
    for (int i = 0; i < 30; i++) {
        world_points.push_back(cv::Point3f(5 * (i / 3), 4 * (i % 3), 0.0f));
    }

    // Perform calibration
    // Flags are set out so they can be commented out and "freed" easily
    int calibration_flags = 0
        | cv::CALIB_FIX_K1
        | cv::CALIB_FIX_K2
        | cv::CALIB_FIX_K3
        | cv::CALIB_FIX_K4
        | cv::CALIB_FIX_K5
        | cv::CALIB_FIX_K6
        | cv::CALIB_ZERO_TANGENT_DIST
        | 0;

    // Initialise matrix
    cv::Mat intrinsic_matrix = cv::Mat(3, 3, CV_64F);
    intrinsic_matrix.ptr<float>(0)[0] = 1;
    intrinsic_matrix.ptr<float>(1)[1] = 1;
    cv::Mat distortion_coeffs = cv::Mat::zeros(5, 1, CV_64F);

    // Rotation and translation vectors
    std::vector<cv::Mat> undistort_rvecs;
    std::vector<cv::Mat> undistort_tvecs;

    // Wrap in an outer vector for calibration
    std::vector<std::vector<cv::Point2f>>im_points_v(1, im_points);
    std::vector<std::vector<cv::Point3f>>w_points_v(1, world_points);

    // Calibrate; only 1 plane, so intrinsics can't be trusted
    cv::Size image_size(4000, 3000);
    calibrateCamera(w_points_v, im_points_v,
        image_size, intrinsic_matrix, distortion_coeffs, 
        undistort_rvecs, undistort_tvecs, calibration_flags);

    // Undistort im_points
    std::vector<cv::Point2f> ud_points;
    cv::undistortPoints(im_points, ud_points, intrinsic_matrix, distortion_coeffs);

    // ud_points have been "unintrinsiced", but we don't know the intrinsics, so reverse that   
    double fx = intrinsic_matrix.at<double>(0, 0);
    double fy = intrinsic_matrix.at<double>(1, 1);
    double cx = intrinsic_matrix.at<double>(0, 2);
    double cy = intrinsic_matrix.at<double>(1, 2);

    for (std::vector<cv::Point2f>::iterator iter = ud_points.begin(); iter != ud_points.end(); iter++) {
        iter->x = iter->x * fx + cx;
        iter->y = iter->y * fy + cy;
    }

    // Find a homography mapping the undistorted points to the known world points, ground plane
    cv::Mat homography = cv::findHomography(ud_points, world_points);

    // Transform the undistorted image points to the world points (2d only, but z is constant)
    std::vector<cv::Point2f> estimated_world_points;    
    std::cout << "homography" << homography << std::endl;
    cv::perspectiveTransform(ud_points, estimated_world_points, homography);

    // Work out error
    double sum_sq_error = 0;
    for (int i = 0; i < 30; i++) {
        double err_x = estimated_world_points.at(i).x - world_points.at(i).x;
        double err_y = estimated_world_points.at(i).y - world_points.at(i).y;

        sum_sq_error += err_x*err_x + err_y*err_y;
    }
    std::cout << "Sum squared error is: " << sum_sq_error << std::endl;

Answer 1

I would take random samples of the 30 input points and compute the homography in each case along with the errors under the estimated homographies, a RANSAC scheme, and verify consensus between error levels and homography parameters, this can be just a verification of the global optimisation process. I know that might seem unnecessary, but it is just a sanity check for how sensitive the procedure is to the input (noise levels, location)

Also, it seems logical that fixing most of the variables gets you the least errors, as the degrees of freedom in the minimization process are less. I would try fixing different ones to establish another consensus. At least this would let you know which variables are the most sensitive to the noise levels of the input.

Hopefully, such a small section of the image would be close to the image centre as it will incur the least amount of lens distortion. Is using a different distortion model possible in your case? A more viable way is to adapt the number of distortion parameters given the position of the pattern with respect to the image centre.

Without knowing the constraints of the algorithm, I might have misunderstood the question, that's also an option too, in such case I can roll back.

I would like to have this as a comment rather, but I do not have enough points.

Answer 2

OpenCV runs Levenberg-Marquardt algorithm inside calibrate camera.

https://en.wikipedia.org/wiki/Levenberg%E2%80%93Marquardt_algorithm/

This algortihm works fine in problems with one minimum. In case of single image, points located close each other and many dimensional problem (n= number of coefficents) algorithm may be unstable (especially with wrong initial guess of camera matrix. Convergence of algorithm is well described here:

https://na.math.kit.edu/download/papers/levenberg.pdf/

As you wrote, error depends on calibration flags - number of flags changes dimension of a problem to be optimized.

Camera calibration also calculates pose of camera, which will be bad in models with wrong calibration matrix.

As a solution I suggest changing approach. You dont need to calculate camera matrix and pose in this step. Since you know, that points are located on a plane you can use 3d-2d plane projection equation to determine distribution type of points. By distribution I mean, that all points will be located equally on some kind of trapezoid.

Then you can use cv::undistort with different distCoeffs on your test image and calculate image point distribution and distribution error.

The last step will be to perform this steps as a target function for some optimization algorithm with distortion coefficents being optimized.

This is not the easiest solution, but i hope it will help you.