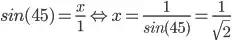Geometry - Calculate distance of point from line

Question

I want to calculate the distance of a point from a line defined by 2 points.

I am using javascript and thats what I came up with using wikipedia: https://en.wikipedia.org/wiki/Distance_from_a_point_to_a_line

function distance(point1, point2, x0, y0) {
    return ((Math.abs((point2.y - point1.y) * x0 - 
                     (point2.x - point1.x) * y0 + 
                     point2.x * point1.y - 
                     point2.y * point1.x)) /
            (Math.pow((Math.pow(point2.y - point1.y, 2) + 
                       Math.pow(point2.x - point1.x, 2)), 
                      0.5)));
}

The problem is that It doesn't seem accurate since if I enter these parameters :

alert(distance({ x: 1, y: 1 }, { x: 2, y: 2 }, 1, 0));

It returns 1/sqrt(2) instead of returning 1 (which is the distance between the point (1, 0) and the line at point (1, 1)

EDIT : I understand the code above does not do what I wanted it to do. It caulcated from a point to a line represented by 2 point but the line is INFINITE (I wanted something more like a vector which has 2 end-point)

I found the answer here

The result is correct. The distance between a point and a line is the shortest distance from the point to the line, or with other words, is the distance on the perpendicular line to the the point. — Zimmi, Jul 18 '15 at 19:20
The javascript is ok, your math is not :-) The closest point from (1,0) on a line through (1,1) and (2,2) is (0.5,0.5). — m69's been on strike for years, Jul 18 '15 at 19:20
It would probably help to plot out the line, point, and perpendicular from the point to the line. — Roshan Mathews, Jul 18 '15 at 19:29
The calculations are correct when you understand that it is the distance between a point and a perpetual line that continues till infinity in each direction. Without an endpoint, the closest point is the one calculated. If you need to go to an end-point of a _line-segment_ you'll need different code. :) — enhzflep, Jul 18 '15 at 19:59
I understand what you guys are saying but I didn't understand the equation correctly, I want something that will give me the shortest distance from the point to the line — Or Betzalel, Jul 18 '15 at 20:40
@OrBetzalel 1/sqrt(2) is the shortest distance from the point to the line. I don't know what's unclear. — NilsB, Jul 18 '15 at 20:44
possible duplicate of [Shortest distance between a point and a line segment](http://stackoverflow.com/questions/849211/shortest-distance-between-a-point-and-a-line-segment) — Peter O., Jul 18 '15 at 21:43

NilsB · Accepted Answer · 2015-07-18T20:41:42.610

I think 1/sqrt(2) = 0.7071... is quite right. See the image: enter image description here

Edit:

var board = JXG.JSXGraph.initBoard('jxgbox', {
  boundingbox: [-1, 3, 3, 0],
  keepaspectratio: true,
  axis: true
});

var f1 = function(x) {
  return x;
};

board.create('functiongraph', [f1]);

board.create('point', [1, 1], {
  size: 4,
  name: '1,1'
});
board.create('point', [2, 2], {
  size: 4,
  name: '2,2'
});
var p1 = board.create('point', [1, 0], {
  size: 4,
  name: '1,0'
});
var p2 = board.create('point', [0.5, 0.5], {
  size: 0,
  name: '1,0'
});
var li2 = board.create('line', [p1, p2], {
  straightFirst: false,
  straightLast: false,
  strokeWidth: 2,
  dash: 2
});

<html>

<head>
  <link rel="stylesheet" type="text/css" href="http://jsxgraph.uni-bayreuth.de/distrib/jsxgraph.css" />
  <script type="text/javascript" src="http://jsxgraph.uni-bayreuth.de/distrib/jsxgraphcore.js"></script>
</head>

<body>
  <div id="jxgbox" class="jxgbox" style="width:500px; height:600px;"></div>
</body>

</html>

Just out of interest, how did you draw this image / plot? – Lasse Christiansen Jul 18 '15 at 20:04 — Lasse Christiansen, Jul 18 '15 at 20:04

score 1 · Answer 2 · answered Jul 18 '15 at 20:32

To add a mathematical point of view, here follows a mathematical "proof" of why your function is correct:

The shortest distance between a point and a line is the distance on the perpendicular line to the point. In this case we know that the angle between the line and the x-axis is 45 degrees and we know that the distance from origo to (1, 0) equals 1.

Using:

formula

... we see that your result is correct, since sin(angle) = the opposite side of a right-angled triangle / hypotenuse.

Geometry - Calculate distance of point from line

2 Answers2