Here are two ideas: an O(n) approximation algorithm and an O(n^2 log n) exact (non-approximate) algorithm:
Fast approximation
Use locality-sensitive hashing. Basically, hash each point to a hash bucket that contains all nearby points. The buckets are set up so that collisions only happen between nearby points - unlike similarly-named hash tables, collisions are useful here. Keep a running count of the number of collisions in a bucket, and then use the center of that bucket as the center of your circle.
I admit that this is a fast explanation of a concept that is not super-obvious the first time you hear of it. An analogy would be to ask a bunch of people what their zip code is, and use the most common zip code to determine the most populous circle. It's not perfect, but a good fast heuristic.
It's basically linear time in terms of the number of points, and you can update your data set on the fly to incrementally get new answers in constant time per point (constant with respect to n = number of points).
More about locality-sensitive hashes in general or about my personal favorite version that would work in this case.
Better-than-brute-force deterministic approach
The idea is: for each point, place the edge of a circle on that point and sweep the circle around to see which direction contains the most points. Do this for all points and we find the global max.
The sweep around a point p can be done in n log n time by: (a) finding the angle interval per other point q such that when we place the circle at angle theta, then it contains q; and (b) sorting the intervals so that we can march/sweep around p in linear time.
So it takes O(n log n) time to find the best circle touching a fixed point p, and then multiply that by O(n) to perform the check for all points. The total time is O(n^2 log n).

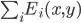 .
.