69

Can some one tell me the difference between hamiltonian path and euler path. They seem similar!

Guy Coder
  • 24,501
  • 8
  • 71
  • 136
mousey
  • 11,601
  • 16
  • 52
  • 59
  • 6
    I have removed the C/C++ tags. Feel free to add them back if you are actually looking for some sort of code for algorithms regarding euler/hamiltonian paths. –  Jul 16 '10 at 22:10
  • 1
    A path contains each vertex exactly once (exception may be the first/ last vertex in case of a closed path/cycle). So the term **Euler Path** or **Euler Cycle** seems misleading to me. It should be **Euler Trail** or **Euler Circuit**. – Md. Abu Nafee Ibna Zahid Mar 06 '18 at 14:24
  • I agree with Md. Abu Nafee. the name `Euler path` seems misleading as vertices are repeated in it. Its original name is `Eulerian trail`. `Euler path` is a misnomer. – srbcheema1 Dec 04 '18 at 21:08

9 Answers9

134

An Euler path is a path that passes through every edge exactly once. If it ends at the initial vertex then it is an Euler cycle.

A Hamiltonian path is a path that passes through every vertex exactly once (NOT every edge). If it ends at the initial vertex then it is a Hamiltonian cycle.

In an Euler path you might pass through a vertex more than once.

In a Hamiltonian path you may not pass through all edges.

Peter
  • 437
  • 1
  • 4
  • 20
Chris Diver
  • 19,362
  • 4
  • 47
  • 58
  • 2
    from: http://pballew.net/graphs.html Notice that for an Euler path you may visit each vertex more than once and in a Hamilton path it is not necessary to travel every edge. – NG. Jul 16 '10 at 21:41
  • 4
    IIRC, it's easy to find if there's a Euler path (or cycle), but whether a graph has a Hamiltonian is NP-complete. – David Thornley Jul 16 '10 at 21:58
  • Yes, I believe there are certain properties of a Euler path which you can use to prove a graph has a Euler path without an algorithm to traverse it. Finding a Hamiltonian path is an NP-complete, i think the algorithm involves trial and error. I thought this would be beyond the scope of the original question to add it to the answer, the OP is obviously new to graph theory :D It's been a while for me, I might dig out my old books. – Chris Diver Jul 17 '10 at 02:48
  • 2
    A path contains each vertex exactly once (exception may be the first/ last vertex in case of a closed path/cycle). So the term **Euler Path** or **Euler Cycle** seems misleading to me. It should be **Euler Trail** or **Euler Circuit**. – Md. Abu Nafee Ibna Zahid Mar 06 '18 at 14:23
  • 1
    I agree with Md. Abu Nafee. the name `Euler path` seems misleading as vertices are repeated in it. Its original name is `Eulerian trail`. `Euler path` is a misnomer. – srbcheema1 Dec 04 '18 at 21:09
  • Interesting trivia. I created and added the tag [euler-path](https://stackoverflow.com/tags/euler-path/info) and because of this answer you now top the list of *Top Answers* for Euler path at SO. :) – Guy Coder Jan 16 '20 at 11:47
  • Good and clear answer! – alan23273850 Jul 11 '23 at 08:19
12

Graph Theory Definitions

(In descending order of generality)

  • Walk: a sequence of edges where the end of one edge marks the beginning of the next edge

  • Trail: a walk which does not repeat any edges. All trails are walks.

  • Path: a walk where each vertex is traversed at most once. (paths used to refer to open walks, the definition has changed now) The property of traversing vertices at most once means that edges are also crossed at most once, hence all paths are trails.

Hamiltonian paths & Eulerian trails

  • Hamiltonian path: visits every vertex in the graph (exactly once, because it is a path)

  • Eulerian trail: visits every edge in the graph exactly once (because it is a trail, vertices may well be crossed more than once.)

Luc
  • 83
  • 1
  • 3
Will
  • 1,413
  • 1
  • 15
  • 13
  • 2
    +1 for considering the definition of **Path** (Each vertex traversed exactly once). The term **Euler Path** or **Euler Cycle** seems misleading to me. It should always be **Euler Trail** or **Euler Circuit**. Unfortunately other answers didn't consider the definition of **Path**. – Md. Abu Nafee Ibna Zahid Mar 06 '18 at 14:47
  • 1
    Please add links to the official sources of these definitions. – root-11 Mar 09 '20 at 14:56
9

Eulerian path must visit each edge exactly once, while Hamiltonian path must visit each vertex exactly once.

Roman Cheplyaka
  • 37,738
  • 7
  • 72
  • 121
  • A **Path** contains each vertex exactly once (exception may be the first/ last vertex in case of a closed path/cycle). So the term **Euler Path** or **Euler Cycle** seems misleading to me. It should be **Euler Trail** or **Euler Circuit**. – Md. Abu Nafee Ibna Zahid Mar 06 '18 at 14:27
  • Please add links to the official sources of these definitions. – root-11 Mar 09 '20 at 14:56
4

They are related but are neither dependent nor mutually exclusive. If a graph has an Eurler cycle, it may or may not also have a Hamiltonian cyle and vice versa.

Euler cycles visit every edge in the graph exactly once. If there are vertices in the graph with more than two edges, then by definition, the cycle will pass through those vertices more than once. As a result, vertices can be repeated but edges cannot.

Hamiltonian cycles visit every vertex in the graph exactly once (similar to the travelling salesman problem). As a result, neither edges nor vertices can be repeated.

advait
  • 6,355
  • 4
  • 29
  • 39
  • 1
    You are conflating paths and circuits. A Hamiltonian/Eulerian circuit is a path/trail of the appropriate type that also starts and ends at the same node. – Yaniv Feb 08 '13 at 00:47
  • 1
    A **Path** contains each vertex exactly once (exception may be the first/ last vertex in case of a closed path/cycle). So the term **Euler Path** or **Euler Cycle** seems misleading to me. It should be **Euler Trail** or **Euler Circuit**. – Md. Abu Nafee Ibna Zahid Mar 06 '18 at 14:30
4

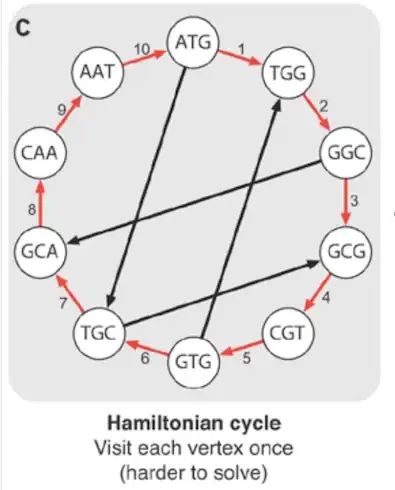
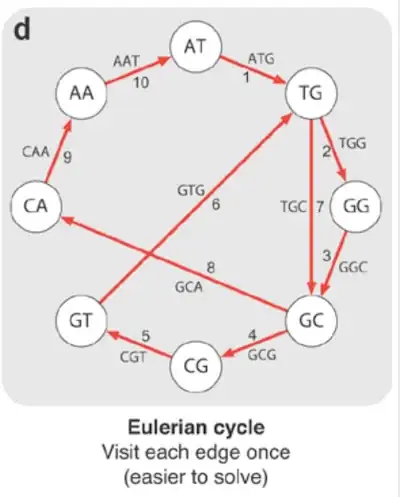
I'll use a common example in biology; reconstructing a genome by making DNA samples.

De-novo assembly

To construct a genome from short reads, it's necessary to construct a graph of those reads. We do it by breaking the reads into k-mers and assemble them into a graph.

enter image description here

We can reconstruct the genome by visiting each node once as in the diagram. This is known as Hamiltonian path.

Unfortunately, constructing such path is NP-hard. It's not possible to derive an efficient algorithm for solving it. Instead, in bioinformatics we construct a Eulerian cycle where an edge represents an overlap.

enter image description here

ABCD
  • 7,914
  • 9
  • 54
  • 90
3

A Hamiltonian path visits every node (or vertex) exactly once, and a Eulerian path traverses every edge exactly once.

burningstar4
  • 233
  • 2
  • 6
  • A **Path** contains each vertex exactly once (exception may be the first/ last vertex in case of a closed path/cycle). So the term **Euler Path** or **Euler Cycle** seems misleading to me. It should be **Euler Trail** or **Euler Circuit**. – Md. Abu Nafee Ibna Zahid Mar 06 '18 at 14:31
1

An Euler path is a path that uses every edge of a graph exactly once.and it must have exactly two odd vertices.the path starts and ends at different vertex. A Hamiltonian cycle is a cycle that contains every vertex of the graph hence you may not use all the edges of the graph.

Mibei nicholas
  • 11
  • 1
1

Euler Path - An Euler path is a path in which each edge is traversed exactly once.

Hamiltonian Path - An Hamiltonian path is path in which each vertex is traversed exactly once.

If you have ever confusion remember E - Euler E - Edge.

randomUser
  • 653
  • 6
  • 23
0

Euler path is a graph using every edge(NOTE) of the graph exactly once. Euler circuit is a euler path that returns to it starting point after covering all edges.

While hamilton path is a graph that covers all vertex(NOTE) exactly once. When this path returns to its starting point than this path is called hamilton circuit.

Jeffrey Blake
  • 9,659
  • 6
  • 43
  • 65
Rajan Chauha n
  • 11