I want to create a matrix from a vector by concatenating the vector onto itself n times. So if my vector is mx1, then my matrix will be mxn and each column of the matrix will be equal to the vector.
Which of the following is the best/correct way, or maybe there is a better way I do not know?
matrix = repmat(vector, 1, n);
matrix = vector * ones(1, n);
Thanks
Here is some benchmarking using timeit with different vector sizes and repetition factors. The results to be shown are for Matlab R2015b on Windows.
First define a function for each of the considered approaches:
%// repmat approach
function matrix = f_repmat(vector, n)
matrix = repmat(vector, 1, n);
%// multiply approach
function matrix = f_multiply(vector, n)
matrix = vector * ones(1, n);
%// indexing approach
function matrix = f_indexing(vector,n)
matrix = vector(:,ones(1,n));
Then generate vectors of different size, and use different repetition factors:
M = round(logspace(2,4,15)); %// vector sizes
N = round(logspace(2,3,15)); %// repetition factors
time_repmat = NaN(numel(M), numel(N)); %// preallocate results
time_multiply = NaN(numel(M), numel(N));
time_indexing = NaN(numel(M), numel(N));
for ind_m = 1:numel(M);
for ind_n = 1:numel(N);
vector = (1:M(ind_m)).';
n = N(ind_n);
time_repmat(ind_m, ind_n) = timeit(@() f_repmat(vector, n)); %// measure time
time_multiply(ind_m, ind_n) = timeit(@() f_multiply(vector, n));
time_indexing(ind_m, ind_n) = timeit(@() f_indexing(vector, n));
end
end
The results are plotted in the following two figures, using repmat as reference:
figure
imagesc(time_multiply./time_repmat)
set(gca, 'xtick',1:2:numel(N), 'xticklabels',N(1:2:end))
set(gca, 'ytick',1:2:numel(M), 'yticklabels',M(1:2:end))
title('Time of multiply / time of repmat')
axis image
colorbar
figure
imagesc(time_indexing./time_repmat)
set(gca, 'xtick',1:2:numel(N), 'xticklabels',N(1:2:end))
set(gca, 'ytick',1:2:numel(M), 'yticklabels',M(1:2:end))
title('Time of indexing / time of repmat')
axis image
colorbar
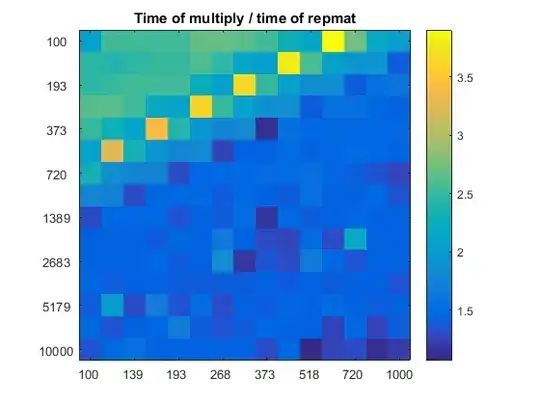
Perhaps a better comparison is to indicate, for each tested vector size and repetition factor, which of the three approaches is the fastest:
figure
times = cat(3, time_repmat, time_multiply, time_indexing);
[~, fastest] = min(times, [], 3);
imagesc(fastest)
set(gca, 'xtick',1:2:numel(N), 'xticklabels',N(1:2:end))
set(gca, 'ytick',1:2:numel(M), 'yticklabels',M(1:2:end))
title('1: repmat is fastest; 2: multiply is; 3: indexing is')
axis image
colorbar
Some conclusions can be drawn from the figures:
repmatrepmat. It tends to be faster for large values of vector size or repetition factor, and slower for small values.
Either method is correct if they provide you with the desired output.
However, depending on how you declare your vector you may get incorrect results with repmat that will be spotted if you use ones. For instance take this example
>> v = 1:10;
>> m = v * ones(1, n)
Error using *
Inner matrix dimensions must agree.
>> m = repmat(v, 1, n)
m =
Columns 1 through 22
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2
Columns 23 through 44
3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 1 2 3 4
Columns 45 through 50
5 6 7 8 9 10
ones provides an error to let you know you aren't doing the right thing but repmat doesn't. Whilst this example works correctly with both repmat and ones
>> v = (1:10).';
>> m = v * ones(1, n)
m =
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
6 6 6 6 6
7 7 7 7 7
8 8 8 8 8
9 9 9 9 9
10 10 10 10 10
>> m = repmat(v, 1, n)
m =
1 1 1 1 1
2 2 2 2 2
3 3 3 3 3
4 4 4 4 4
5 5 5 5 5
6 6 6 6 6
7 7 7 7 7
8 8 8 8 8
9 9 9 9 9
10 10 10 10 10
Both are correct, but repmat is a more general solution for multi-dimensional matrix copying and is thus bound to be slower than an other solution. The specific 'homemade' solution of multiplying two vectors is possibly faster. It is probably even faster to do selecting instead of multiplying, i.e. vector(:,ones(n,1)) instead of vector*ones(1,n).
EDIT:
Type open repmat in your Command Window. As you can see, it is not a built-in function. You can see that it also makes use of ones (selecting) to copy matrices. However, since it is a more general solution (for scalars and multi-dimensional matrices and copies in multiple directions), you will find unnecessary if statements and other unnecessary code, effectively slowing things down.
EDIT:
Multiplying vectors with ones becomes slower for very large vectors. The unequivocal winner is using ones with selection, i.e. vector(:,ones(n,1)) (which should always be faster than repmat since it uses the same strategy).
You can also do this -
vector(:,ones(1,n))
But, if I have to choose, repmat would be the go-to approach for me, as it is made exactly for this purpose. Also, depending on how you are going to use this replicated array, you can just avoid creating it altogether with bsxfun that does on-the-fly replication on its input arrays and some operation to be applied on the inputs. Here's a comparison on that - Comparing BSXFUN and REPMAT that shows bsxfun to be better than repmat in most cases.
For the sake of performance, let's test out these. Here's a benchmarking code to do so -
%// Inputs
vector = rand(1000,1);
n = 1000;
%// Warm up tic/toc.
for iter = 1:50000
tic(); elapsed = toc();
end
disp(' ------- With REPMAT -------')
tic,
for iter = 1:200
A = repmat(vector, 1, n);
end
toc, clear A
disp(' ------- With vector(:,ones(1,n)) -------')
tic,
for iter = 1:200
A = vector(:,ones(1,n));
end
toc, clear A
disp(' ------- With vector * ones(1, n) -------')
tic,
for iter = 1:200
A = vector * ones(1, n);
end
toc
Runtime results -
------- With REPMAT -------
Elapsed time is 1.241546 seconds.
------- With vector(:,ones(1,n)) -------
Elapsed time is 1.212566 seconds.
------- With vector * ones(1, n) -------
Elapsed time is 3.023552 seconds.
