How does O(log log N) complexity loop look like?

Question

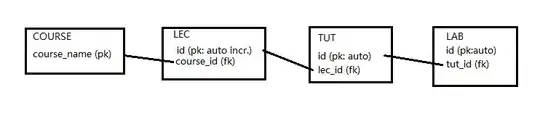
I have a very basic question here

for(int i = 1; i < N/2; i++) {

}

My initial understanding was the time-complexity for the above loop would O(logn) but after reading through some articles it is pretty much evident that it's simply O(n) and O(logn) would look like for (i = 1; i <= n; i *= 2)

Now my question is how does O(log log N) loop look like?

http://stackoverflow.com/questions/5201013/on-log-log-n-time-complexity — surya singh, Oct 03 '15 at 12:18
Where did you see that the above loop is O(log N)? It is not. — Henry, Oct 03 '15 at 12:18

score 7 · Accepted Answer · answered Oct 03 '15 at 12:37

7

O(log n) loop:

for (i = 1; i <= n; i *= 2)

So you double i at each step. Basically:

Increment => O(n)
Doubling => O(log n)
??? => O(log log n)

What comes after multiplication? Exponentiation. So this would be O(log log n):

for (i = 2; i <= n; i *= i) // we are squaring i at each step

Note: your loop is O(n), not O(log n). Keeping in line with the increment / double / exponentiate idea above, you can rewrite your loop using incrementation:

for(int i = 1; i < n; i += 2)

Even if you increment by more, it's still incrementation, and still O(n).

answered Oct 03 '15 at 12:37

IVlad

43,099
13
111
179

1

@piechuckerr `i *= 2`means that `i` is doubled after each iteration of the loop. `N / 2` means that you always work with half of `N`. `N` never changes its value in your case. Take `n= 64` for example. You will iterate for `i = 1, 2, 3, 4, 5, 6, 7, ..., 64 / 2 = 32`. My example will iterate for `i = 1, 2, 4, 8, 16, 32, 64`. Notice the difference? – IVlad Oct 03 '15 at 14:26

borancar · Answer 2 · 2015-10-03T12:26:02.940

That loop doesn't look like O(log N). It is what it is, an O(N/2) loop. To quote the definition:

Function f(x) is said to be O(g(x)) iff (if and only if) there exists a positive real number c, and a real number x0 such that |f(x)| <= c|g(x)| for all x >= x0. For example, you could also call that loop O(N), O(N^2), O(N^3) as you can find the required parameters easily. But, you cannot find parameters that will make O(log N) fit.

As for O(log log N), I suppose you could rewrite Interpolation search implementation given here https://en.wikipedia.org/wiki/Interpolation_search to use a for loop. It is O(log log N) on the average!

score 0 · Answer 3 · answered Oct 03 '15 at 12:44

Your cost is not O(logN) your cost is O(N*logN).

Read the link you will see a function example like :

No matter the number in the beginning of the polynomial cost is the biggest polynomial.

In your case it is

1/2 * n * log(n) , which 1/2 makes no difference your complexity is O(N*logN)

How does O(log log N) complexity loop look like?

3 Answers3