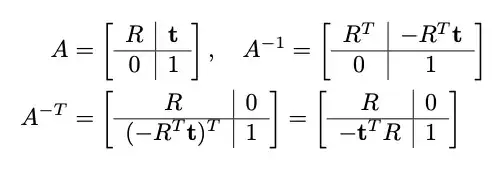Finding nearest neighbours of radial segments

Question

First, don't be scared by the looks of this question ;)

I'm trying to implement a shape descriptor in matlab called Circular Blurred Shape Model, and part of this is to get a list of nearest neighbours for every radial segment as can be seen in Figure 1d)

I went for a straight and simple implementation in MATLAB but I'm stuck at Step 5 and 6 of the algorithm, mainly because I can't wrap my head around the definition:

Xb{c,s} = {b1, ..., b{c*s}} as the sorted set of the elements in B* 
so that d(b*{c,s}, bi*) <= d(b*{c,s}, bj*), i<j

For me this sounds like a cascaded sorting, first sort by ascending distance and then by ascending index, but the nearest neighbours I find are not according to the paper.

As an example I show you the nearest neighbours I obtain for the segment b{4,1}, this is the one marked "EX" in Figure 1d)

I get the following list of nearest neighbors for b{4,1}: b{3,2}, b{3,1}, b{3,8}, b{2,1}, b{2,8}

correct according to the paper would be: b{4,2}, b{4,8}, b{3,2}, b{3,1}, b{3,8}

However my points actually are the closest set to the selected segment measured by euclidean distance! The distance b{4,1} <=> b{2,1} is smaller than b{4,1} <=> b{4,2} or b{4,1} <=> b{4,8}...

And here is my (ugly, but straight forward) MATLAB code:

width  = 734;
height = 734;

assert(width == height, 'Image must be square in size!');

% Radius of the correlogram
R = width;

% Number of circles in correlogram
C = 4;

% Number of sections in correlogram
S = 8;

% "width" of ring segments
d = R/C;

% angle of one segment in degrees
g = 360/S;

% set of bins for the circular description of I
B = zeros(C, S);

% centroid coordinates for bins
B_star = zeros(C,S,2);


% calculate centroids of bins
for c=1:C
    for s=1:S
        alpha = deg2rad(max(s-1, 0)*g + g/2);
        r     = d*max((c-1),0) + d/2;

        B_star(c,s,1) = r*cos(alpha);
        B_star(c,s,2) = r*sin(alpha);
    end
end

% create sorted list of bin numbers which fullfill
% d(b{c,s}*, bi*) <= d(b{c,s}, bj*) where i<j

% B_star_dists is a simple square distance matrix for getting
% the distance between two centroids c_i,s_i and c_j,s_j
B_star_dists = zeros(C*S, C*S);
for i=1:C*S
    [c_i, s_i] = ind2sub([C,S], i);
    % x,y centroid coordinates for point i
    b_star_i   = [B_star(c_i, s_i, 1), B_star(c_i, s_i, 2)];

    for j=1:C*S
        [c_j, s_j] = ind2sub([C,S], j);
        % x,y centroid coordinates for point j
        b_star_j   = [B_star(c_j, s_j, 1), B_star(c_j, s_j, 2)];

        % store the euclidean distance between these two centroids
        % in the distance matrix.
        B_star_dists(i,j) = norm(b_star_i - b_star_j);
    end
end

% calculate nearest neighbour "centroids" for each centroid
% B_NN is a cell array, B{idx} gives an array of indexes to the 
% nearest neighbour centroids. 

B_NN = cell(C*S, 1);
for i=1:C*S
    [c_i, s_i] = ind2sub([C,S], i);

    % get a (C*S)x2 matrix of all distances, the first column are the array
    % indexes and the second column are the distances e.g
    % 1   d1
    % 2   d2
    % ..  ..
    % CS  d{c,s}

    dists = [transpose(1:C*S), B_star_dists(:, i)];

    % sort ascending by the distances first (e.g second column) then
    % sort ascending by the array index (e.g first column)
    dists = sortrows(dists, [2,1]);

    % middle section has nine neighbours, set as default
    neighbour_count = 9;

    if c_i == 1
        % inner region has S+3 neighbours
        neighbour_count = S+3;
    elseif c_i == C
        % outer most ring has 6 neighbours
        neighbour_count = 6;
    end

    B_NN{i} = dists(1:neighbour_count,1);
end

% FROM HERE ON JUST VISUALIZATION CODE

figure(1);
hold on;
for c=1:C
    % plot circles
    r = c*d;
    plot(r*cos(0:pi/50:2*pi), r*sin(0:pi/50:2*pi), 'k:');
end

for s=1:S
    % plot lines

    line_len = C*d;
    alpha    = deg2rad(s*g); 

    start_pt = [0, 0];
    end_pt   = start_pt + line_len.*[cos(alpha), sin(alpha)];

    plot([start_pt(1), end_pt(1)], [start_pt(2), end_pt(2)], 'k-');
end

for c=1:C
    % plot centroids of segments
    for s=1:S
        segment_centroid = B_star(c,s, :);
        plot(segment_centroid(1), segment_centroid(2), '.k');
    end
end

% plot some nearest neighbours
% list of [C;S] 
plot_nn = [4;1];

for i = 1:size(plot_nn,2) 
   start_c = plot_nn(1,i);
   start_s = plot_nn(2,i);

   start_pt = [B_star(start_c, start_s,1), B_star(start_c, start_s,2)];
   start_idx = sub2ind([C, S], start_c, start_s);

   plot(start_pt(1), start_pt(2), 'xb');

   nn_idx_list = B_NN{start_idx};

   for j = 1:length(nn_idx_list)
      nn_idx = nn_idx_list(j); 
      [nn_c, nn_s] = ind2sub([C, S], nn_idx);
      nn_pt = [B_star(nn_c, nn_s,1), B_star(nn_c, nn_s,2)];

      plot(nn_pt(1), nn_pt(2), 'xr');
   end
end

The full paper can be found here

Answer 1

The paper talks about "region neighbours"; the interpretation that these are the "nearest neighbours" in a Euclidian distance sense is incorrect. They are simply regions that are neighbours of a certain region, and the method of finding them is trivial:

The regions have 2 coordinates: (c,s) where c denotes which concentric circle they're part of, from 1 in the center to C at the edge, and s denotes which sector they're part of, from 1 starting at angle 0° to S ending at angle 360°.

Every region whose c and s coordinates differ at most 1 from the region's coordinates, is a neighbouring region (segment numbers wrap around from S to 1.) Depending on the location of the region, there are 3 cases: (as illustrated in fig. 1d)

• The region is a middle region (marked MI) e.g. region b(2,4)
  There are 2 neighbouring circles and 2 neighbouring sectors, so 9 regions in total:
  every region in circle 1, 2 or 3 and sector 3, 4 or 5:
  b(1,3), b(2,3), b(3,3), b(1,4), b(2,4), b(3,4), b(1,5), b(2,5), b(3,5)

• The region is an inner region (marked IN) e.g. region b(1,8)
  There is only one neighbouring circle and 2 neighbouring sectors, but all the inner regions are neighbours, so S + 3 regions in total:
  every region in circle 2 and sector 7, 8 or 1:
  b(2,7), b(2,8), b(2,1)
  and every region in the inner circle:
  b(1,1), b(1,2), b(1,3), b(1,4), b(1,5), b(1,6), b(1,7), b(1,8)

• The region is an external region (marked EX) e.g. region b(3,1)
  There is only one neighbouring circle and 2 neighbouring sectors, so 6 regions in total:
  every region in circle 2 or 3 and sector 8, 1 or 2:
  b(2,8), b(2,1), b(2,2), b(3,8), b(3,1), b(3,2)

Answer 2

To add a bit of matlab to the great answer of @m69, you could automatize the indexing of neighbours like this:

%assume C and S defined according to the answer of @m69
iif=@(varargin) varargin{2*find([varargin{1:2:end}], 1, 'first')}();
ncfun=@(c) iif(c==1,c+1,c==C,c-1,true,[c-1, c+1]);
nsfun=@(s)mod([s-1, s+1]-1,S)+1;
neighbs=@(c,s) [b(c,nsfun(s)), b(ncfun(c),s)', reshape(b(ncfun(c),nsfun(s)),1,[])];

1. The first one defines an inline if for use in anonymous functions, to spare having to define functions in separate files (this would be needed for the c case). This has the syntax iif(condition1,result1,condition2,result2,...), where each condition is tested after one another, and the result corresponding to the first condition yielding true is returned.

2. The second one defines the radial neighbour indices with an if: return [c-1, c+1] unless either of these is undefined (which would lead to array bound violations)

3. The third one defines a periodic indexing for the angular sectors, such that for S=4 nsfun(2)==[1, 3] and nsfun(4)==[3, 1].

4. I just added an example where for a given valid pair of c,s neighbs(c,s) will return the subarray of b(1:C,1:S) which are neighbours: first the up-down/left-right neighbours, then the (up to) four corner ones.

Answer 3

After spending way too many hours on this I figured it out, the trick to calculate the neighboring regions of an element b{c,s} was:

• Take all segments for the neighbouring rings of c, including c itself, i.e c-1, c, c+1, if it's the inner most circle then only c,c+1 if it's the outer most take c-1, c

• Calculate the euclidean distance from b{c,s} to all the selected centroids from the previous step, including the point b{c,s} itself

• Sort the distances in ascending order and take the first N segments.

The descriptor works quite well, however it's rotational invariance depends on the axis with the highest density in certain cases this is very sensitive to noise/occlusion, i.e the descriptor may be +/- 1 rotation off.

Here's the complete CBSM descriptor implementation in MATLAB, not optimized in any way (I heard MATLAB hates for-loops):

csbm.m

function [descriptor] = csbm(I, R, C, S)
    % Input:
    % ------
    % I = The image, binary, must be square in sice
    % R = The radius of the correlogram, could be half the image width
    % C = Number of circles
    % S = Number of segments per circle

    % Output:
    % -------
    % A C*S-by-1 row vector, the descriptor

    [width, height] = size(I);
    assert(width == height, 'Image must be square in size!');

    % "width" of ring segments
    d = R/C;

    % angle of one segment in degrees
    g = 2*pi/S;

    % centroid coordinates for bins
    B_star = zeros(C*S,2);

    % initialize the descriptor
    descriptor = zeros(C*S,1);

    % calculate centroids of bins
    for c=1:C
        for s=1:S
            alpha = max(s-1, 0)*g + g/2;
            r     = d*max((c-1),0) + d/2;
            ind   = (c-1)*S+s; %sub2ind(cs_size, c,s);

            B_star(ind, :) = [r*cos(alpha), r*sin(alpha)];
        end
    end

    % calculate nearest neighbor regions
    B_NN = cell(C*S,1);

    for c=1:C
        min_circle = max(1,c-1);
        max_circle = min(C,c+1);

        start_sel  = (min_circle-1)*S+1;
        end_sel    = (max_circle)*S;

        centroids  = B_star(start_sel:end_sel, :);

        for s=1:S
            current_ind   = (c-1)*S+s;
            centroid      = B_star(current_ind, :);
            num_centroids = length(centroids);
            distances     = sqrt(sum((centroids-repmat(centroid, num_centroids,1)).^2,2));

            distances     = horzcat(distances, transpose((start_sel:end_sel)));
            distances     = sortrows(distances, [1,2]);

            neighbour_count = 9;

            if c == 1
                % inner region has S+3 neighbours
                neighbour_count = S+3;
            elseif c == C
                % outer most ring has 6 neighbours
                neighbour_count = 6;
            end


            B_NN{current_ind} = distances(1:neighbour_count, 2);
        end
    end

    for x=1:width
        x_centered = x-width/2;

        for y=1:width
            if I(x,y) == 0
                continue;
            end

            y_centered = y-width/2;

            % bin the image point
            r = sqrt(x_centered^2 + y_centered^2);
            a = wrapTo2Pi(atan2(y_centered, x_centered));

            % get bin
            c_pixel = max(1, floor(r/d));
            s_pixel = max(1, floor(a/g));

            if c_pixel > C
                continue;
            end

            ind_pixel = (c_pixel-1)*S+s_pixel;
            pt_pixel  = [x_centered, y_centered];

            % get neighbours of this bin
            neighbours = B_NN{ind_pixel};

            % calculate distance to neighbours
            nn_dists   = sqrt(sum((B_star(neighbours, :) - repmat(pt_pixel, length(neighbours), 1)).^2,2));

            D = sum(1./nn_dists);

            % update the probabilities vector
            descriptor(neighbours) = descriptor(neighbours) + 1./(nn_dists.*D);
        end
    end

    % normalize the vector v
    descriptor   = descriptor./sum(descriptor);

    % make it rotationally invariant
    G = zeros(S/2, 2*C);

    for s=1:S/2
        for c=1:C
            G(s,c)   = descriptor((c-1)*S+s);
            G(s,c+C) = descriptor((c-1)*S+s+S/2);
        end
    end

    [~, max_G_idx] = max(sum(G,2));

    L_G = 0;
    R_G = 0;

    for j=1:C
        for k=1:S
            if k > (max_G_idx) && k < (max_G_idx+S/2)
                L_G = L_G + descriptor((j-1)*S+k); 
            elseif k ~= max_G_idx && k ~= (max_G_idx+S/2)
                R_G = R_G + descriptor((j-1)*S+k); 
            end
        end
    end

    if L_G > R_G
        % B is rotated k=i+S/2-1 positions to the left:
        fprintf('rotate %d to the left\n', max_G_idx+S/2-1);
        rotate_by = -(max_G_idx+S/2-1);
    else
        % B is rotated k=i-1 positions to the right:
        fprintf('rotate %d to the right\n', max_G_idx-1);
        rotate_by = -(max_G_idx-1);
    end

    % segments are grouped by circle
    % so for every circle we get all segments and circular shift them
    for c=1:C
       range_sel = ((c-1)*S+1):(c*S);
       segments  = descriptor(range_sel);
       descriptor(range_sel) = circshift(segments, [rotate_by,0]);
    end
end

plot_descriptor.m

function plot_descriptor(R,C,S, descriptor)
    % Input:
    % ------
    % R Radius for the correlogram in pixels, can be arbitrary
    % C Number of circles
    % S Number of segments per circle
    % descriptor The C*S-by-1 descriptor vector


    % "width" of ring segments
    d = R/C;

    % angle of one segment in degrees
    g = 2*pi/S;

    % full image
    [x,y] = meshgrid(-R:R);
    [theta, rho] = cart2pol(x,y);
    theta = wrapTo2Pi(theta);
    brightness   = zeros(size(rho));

    min_val     = min(descriptor);
    max_val     = max(descriptor);
    scale_fact  = 1/(max_val-min_val);

    for c=1:C
        rInner = (c-1)*d;
        rOuter = c*d;

        for s=1:S
            idx = (c-1)*S+s;

            minTheta = (s-1)*g;
            maxTheta = (s*g);

            matching_theta = find(theta > minTheta & theta < maxTheta);
            matching_rho   = find(rho > rInner & rho < rOuter);
            matching_idx   = intersect(matching_theta, matching_rho);

            intensity = descriptor(idx)*scale_fact;

            brightness(matching_idx) = intensity;
        end
    end

    figure; imshow(mat2gray(brightness));

How to run:

I = imread('bat-18.gif');
I = transpose(im2bw(I, graythresh(I)));
I = edge(I);

[width, height] = size(I);
R = width/2;
C = 24;
S = 24;

descriptor = csbm(I, R, C, S);
plot_descriptor(R,C,S,descriptor);

The output:

Just for the kicks, some scary pictures occured while coding it: