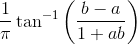I need to write a program that generates random realizations of the Cauchy distribution
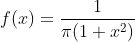
with null location and unit scale.
Also I need to make a histogram between -5 and 5 bins, for a random realization of 1,000 points, together with the theoretical curve making sure they have the same units.
I calculated the cumulative distribution function 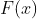 for the Cauchy distribution:
for the Cauchy distribution:
![F(x)=tan[{\pi{(rand()-{\frac{1}{2})}}}]](../../images/2262179263.webp)
And I wrote the following python code:
from __future__ import division
import scipy
import random
import matplotlib.pyplot as plt
import numpy as np
import math as m
valuesX = []
for q in range(1000):
R = random.random()
x = m.tan(m.pi*(R-0.5)) #Cumulative Function
valuesX.append(x)
z = np.linspace(-10,10,1000)
y = 1/(m.pi*(1+z**2)) #Theoretical Cauchy
plt.plot(y,z)
plt.hist(valuesX, bins = 50, range = [-5,5], normed=True)
I don't know if this is acceptable since I'm plotting discrete values (random realization) against a probability density function. How could I compare the two of them? since I need to find the fractional difference for the plot above and determine the global rms deviations between both curves as a function of the size of the random realization.