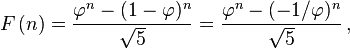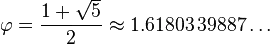How to generate Fibonacci faster

Question

I am a CSE student and preparing myself for programming contest.Now I am working on Fibonacci series. I have a input file of size about some Kilo bytes containing positive integers. Input formate looks like

3 5 6 7 8 0

A zero means the end of file. Output should like

2 
5 
8 
13 
21 

my code is

#include<stdio.h>

int fibonacci(int n) {
  if (n==1 || n==2)
    return 1;
  else
    return fibonacci(n-1) +fibonacci(n-2);
}
int main() {
  int z;
  FILE * fp;    
  fp = fopen ("input.txt","r");    
  while(fscanf(fp,"%d", &z) && z) 
   printf("%d \n",fibonacci(z));
  return 0;
}

The code works fine for sample input and provide accurate result but problem is for my real input set it is taking more time than my time limit. Can anyone help me out.

Answer 1

You could simply use a tail recursion version of a function that returns the two last fibonacci numbers if you have a limit on the memory.

int fib(int n)
{
    int a = 0;
    int b = 1;
    while (n-- > 1) {
        int t = a;
        a = b;
        b += t;
    }
    return b;
}

This is O(n) and needs a constant space.

Answer 2

You should probably look into memoization.

http://en.wikipedia.org/wiki/Memoization

It has an explanation and a fib example right there

Answer 3

You can do this by matrix multiplictation, raising the matrix to power n and then multiply it by an vector. You can raise it to power in logaritmic time.

I think you can find the problem here. It's in romanian but you can translate it with google translate. It's exactly what you want, and the solution it's listed there.

Answer 4

Your algorithm is recursive, and approximately has O(2^N) complexity.

This issue has been discussed on stackoverflow before: Computational complexity of Fibonacci Sequence

There is also a faster implementation posted in that particular discussion.

Answer 5

Look in Wikipedia, there is a formula that gives the number in the Fibonacci sequence with no recursion at all

Answer 6

Use memoization. That is, you cache the answers to avoid unnecessary recursive calls.

Here's a code example:

#include <stdio.h>

int memo[10000]; // adjust to however big you need, but the result must fit in an int
                 // and keep in mind that fibonacci values grow rapidly :)

int fibonacci(int n) {
  if (memo[n] != -1)
    return memo[n];

  if (n==1 || n==2)
    return 1;
  else
    return memo[n] = fibonacci(n-1) +fibonacci(n-2);
}
int main() {
  for(int i = 0; i < 10000; ++i)
    memo[i] = -1;
  fibonacci(50);
}

Answer 7

Nobody mentioned the 2 value stack array version, so I'll just do it for completeness.

// do not call with i == 0
uint64_t Fibonacci(uint64_t i)
{
  // we'll only use two values on stack,
  // initialized with F(1) and F(2)
  uint64_t a[2] = {1, 1};

  // We do not enter loop if initial i was 1 or 2 
  while (i-- > 2)
    // A bitwise AND allows switching the storing of the new value
    // from index 0 to index 1.
    a[i & 1] = a[0] + a[1];

    // since the last value of i was 0 (decrementing i),
    // the return value is always in a[0 & 1] => a[0].
  return a[0];
}                                                                

This is a O(n) constant stack space solution that will perform slightly the same than memoization when compiled with optimization.

// Calc of fibonacci f(99), gcc -O2
Benchmark            Time(ns)    CPU(ns) Iterations
BM_2stack/99                2          2  416666667
BM_memoization/99           2          2  318181818

The BM_memoization used here will initialize the array only once and reuse it for every other call.

The 2 value stack array version performs identically as a version with a temporary variable when optimized.

Answer 8

You can also use the fast doubling method of generating Fibonacci series Link: fastest-way-to-compute-fibonacci-number

It is actually derived from the results of the matrix exponentiation method.

Answer 9

Use the golden-ratio

Answer 10

Matrix multiplication, no float arithmetic, O(log N) time complexity assuming integer multiplication/addition is done in constant time.

Here goes python code

def fib(n):
    x,y = 1,1
    mat = [1,1,1,0]
    n -= 1
    while n>0:
        if n&1==1:
            x,y = x*mat[0]+y*mat[1], x*mat[2]+y*mat[3]
        n >>= 1
        mat[0], mat[1], mat[2], mat[3] = mat[0]*mat[0]+mat[1]*mat[2], mat[0]*mat[1]+mat[1]*mat[3], mat[0]*mat[2]+mat[2]*mat[3], mat[1]*mat[2]+mat[3]*mat[3]
    return x

Answer 11

In C#:

        static int fib(int n)
        {
            if (n < 2) return n;
            if (n == 2) return 1;
            int k = n / 2;
            int a = fib(k + 1);
            int b = fib(k);
            if (n % 2 == 1)
                return a * a + b * b;
            else
                return b * (2 * a - b);
        }

Answer 12

Build an array Answer[100] in which you cache the results of fibonacci(n). Check in your fibonacci code to see if you have precomputed the answer, and use that result. The results will astonish you.

Answer 13

Are you guaranteed that, as in your example, the input will be given to you in ascending order? If so, you don't even need memoization; just keep track of the last two results, start generating the sequence but only display the Nth number in the sequence if N is the next index in your input. Stop when you hit index 0.

Something like this:

int i = 0;
while ( true ) {
    i++; //increment index
    fib_at_i = generate_next_fib()
    while ( next_input_index() == i ) {
        println fib_at_i
}

I leave exit conditions and actually generating the sequence to you.

Answer 14

use any of these: Two Examples of recursion, One with for Loop O(n) time and one with golden ratio O(1) time:

private static long fibonacciWithLoop(int input) {
    long prev = 0, curr = 1, next = 0;      
    for(int i = 1; i < input; i++){
        next = curr + prev;
        prev = curr;
        curr = next;
    }
    return curr;
}

public static long fibonacciGoldenRatio(int input) {
    double termA = Math.pow(((1 + Math.sqrt(5))/2), input);
    double termB = Math.pow(((1 - Math.sqrt(5))/2), input);
    double factor = 1/Math.sqrt(5);
    return Math.round(factor * (termA - termB));
}

public static long fibonacciRecursive(int input) {
    if (input <= 1) return input;
    return fibonacciRecursive(input - 1) + fibonacciRecursive(input - 2);
}

public static long fibonacciRecursiveImproved(int input) {
    if (input == 0) return 0;
    if (input == 1) return 1;
    if (input == 2) return 1;
    if (input >= 93) throw new RuntimeException("Input out of bounds");
    // n is odd
    if (input % 2 != 0) {
        long a = fibonacciRecursiveImproved((input+1)/2);
        long b = fibonacciRecursiveImproved((input-1)/2);
        return a*a + b*b;
    }

    // n is even
    long a = fibonacciRecursiveImproved(input/2 + 1);
    long b = fibonacciRecursiveImproved(input/2 - 1);
    return a*a - b*b;
}

Answer 15

using namespace std;

void mult(LL A[ 3 ][ 3 ], LL B[ 3 ][ 3 ]) {

     int i,

         j,

         z;

     LL C[ 3 ][ 3 ];

     memset(C, 0, sizeof( C ));

     for(i = 1; i <= N; i++)

         for(j = 1; j <= N; j++) {

             for(z = 1; z <= N; z++)

                 C[ i ][ j ] = (C[ i ][ j ] + A[ i ][ z ] * B[ z ][ j ] % mod ) % mod;
         }

     memcpy(A, C, sizeof(C));
};

void readAndsolve() {

    int i;

    LL k;

    ifstream I(FIN);
    ofstream O(FOUT);

    I>>k;

    LL A[3][3];
    LL B[3][3];

    A[1][1] = 1; A[1][2] = 0;
    A[2][1] = 0; A[2][2] = 1;

    B[1][1] = 0; B[1][2] = 1;
    B[2][1] = 1; B[2][2] = 1;

    for(i = 0; ((1<<i) <= k); i++) {

          if( k & (1<<i) ) mult(A, B);

          mult(B, B);
    }

    O<<A[2][1];
}

//1,1,2,3,5,8,13,21,33,...

int main() {

    readAndsolve();

    return(0);
}

Answer 16

public static int GetNthFibonacci(int n)
    {
        var previous = -1;
        var current = 1;
        int element = 0;

        while (1 <= n--)
        {
            element = previous + current;
            previous = current;
            current = element;
        }

        return element;
    }

Answer 17

You can reduce the overhead of the if statement: Calculating Fibonacci Numbers Recursively in C

Answer 18

First of all, you can use memoization or an iterative implementation of the same algorithm.

Consider the number of recursive calls your algorithm makes:

fibonacci(n) calls fibonacci(n-1) and fibonacci(n-2)
fibonacci(n-1) calls fibonacci(n-2) and fibonacci(n-3)
fibonacci(n-2) calls fibonacci(n-3) and fibonacci(n-4)

Notice a pattern? You are computing the same function a lot more times than needed.

An iterative implementation would use an array:

int fibonacci(int n) {
    int arr[maxSize + 1]; 
    arr[1] = arr[2] = 1; // ideally you would use 0-indexing, but I'm just trying to get a point across
    for ( int i = 3; i <= n; ++i )
        arr[i] = arr[i - 1] + arr[i - 2]; 

    return arr[n];
}

This is already much faster than your approach. You can do it faster on the same principle by only building the array once up until the maximum value of n, then just print the correct number in a single operation by printing an element of your array. This way you don't call the function for every query.

If you can't afford the initial precomputation time (but this usually only happens if you're asked for the result modulo something, otherwise they probably don't expect you to implement big number arithmetic and precomputation is the best solution), read the fibonacci wiki page for other methods. Focus on the matrix approach, that one is very good to know in a contest.

Answer 19

#include<stdio.h>

 int g(int n,int x,int y)
   {
   return n==0 ? x : g(n-1,y,x+y);}

 int f(int n)
   {
   return g(n,0,1);}

 int main (void)
   {  
   int i;
   for(i=1; i<=10 ; i++)
     printf("%d\n",f(i)
   return 0;
   }

Answer 20

In the functional programming there is a special algorithm for counting fibonacci. The algorithm uses accumulative recursion. Accumulative recursion are used to minimize the stack size used by algorithms. I think it will help you to minimize the time. You can try it if you want.

int ackFib (int n, int m, int count){
    if (count == 0)
        return m;
    else
        return ackFib(n+m, n, count-1);
}



int fib(int n)
{
 return ackFib (0, 1, n+1);
}

Answer 21

This is similar to answers given before, but with some modifications. Memorization, as stated in other answers, is another way to do this, but I dislike code that doesn't scale as technology changes (size of an unsigned int varies depending on the platform) so the highest value in the sequence that can be reached may also vary, and memorization is ugly in my opinion.

#include <iostream>

using namespace std;

void fibonacci(unsigned int count) {
   unsigned int x=0,y=1,z=0;
   while(count--!=0) {
      cout << x << endl;  // you can put x in an array or whatever
      z = x;
      x = y;
      y += z;
   }
}

int main() {
   fibonacci(48);// 48 values in the sequence is the maximum for a 32-bit unsigend int
   return 0;
}

Additionally, if you use <limits> its possible to write a compile-time constant expression that would give you the largest index within the sequence that can be reached for any integral data type.

Answer 22

#include<stdio.h>
main()
{
 int a,b=2,c=5,d;
   printf("%d %d ");
do
{
   d=b+c;
     b=c;
    c=d;
   rintf("%d ");
  }