Using Matplotlib, I want to get one plot that connects multiple points. The plot commands are within a for loop. Right now, I am getting one figure each, and having to close the first one to open the second.
The desired effect is shown in this Matlab graph:
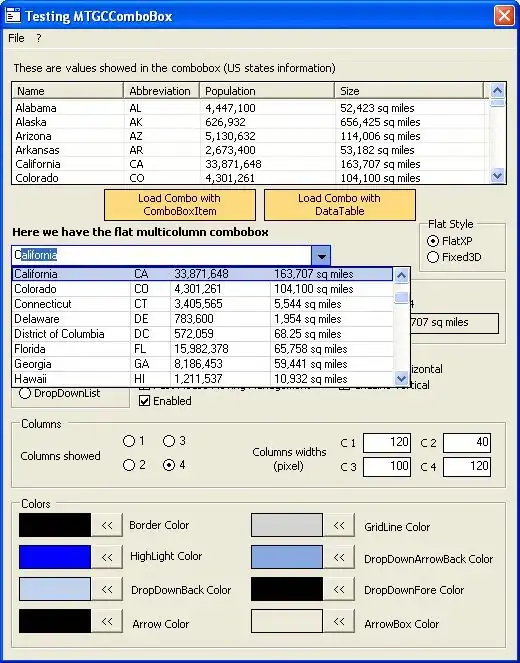
Each point is at an even-numbered N.
How do I do this by modifying my current Python code? The important pieces are the last 4 lines, and the very first for loop on Line 7.
Code:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import odeint
y = 5
x = 2
for N in range(x,x+y,2):
#Constants and parameters
epsilon = 0.01
K00 = np.logspace(0,3,10,10)
len1 = len(K00)
y0 = [0]*(3*N/2+3)
Kplot = np.zeros((len1,1))
Pplot = np.zeros((len1,1))
S = [np.zeros((len1,1)) for kkkk in range(N/2+1)]
KS = [np.zeros((len1,1)) for kkkk in range(N/2)]
PS = [np.zeros((len1,1)) for kkkk in range(N/2)]
Splot = [np.zeros((len1,1)) for kkkk in range(N/2+1)]
KSplot = [np.zeros((len1,1)) for kkkk in range(N/2)]
PSplot = [np.zeros((len1,1)) for kkkk in range(N/2)]
for series in range(0,len1):
K0 = K00[series]
Q = 10
r1 = 0.0001
r2 = 0.001
a = 0.001
d = 0.001
k = 0.999
S10 = 1e5
P0 = 1
tf = 1e10
time = np.linspace(0,tf,len1)
#Defining dy/dt's
def f(y,t):
for alpha in range(0,(N/2+1)):
S[alpha] = y[alpha]
for beta in range((N/2)+1,N+1):
KS[beta-N/2-1] = y[beta]
for gamma in range(N+1,3*N/2+1):
PS[gamma-N-1] = y[gamma]
K = y[3*N/2+1]
P = y[3*N/2+2]
# The model equations
ydot = np.zeros((3*N/2+3,1))
B = range((N/2)+1,N+1)
G = range(N+1,3*N/2+1)
runsumPS = 0
runsum1 = 0
runsumKS = 0
runsum2 = 0
for m in range(0,N/2):
runsumPS = runsumPS + PS[m]
runsum1 = runsum1 + S[m+1]
runsumKS = runsumKS + KS[m]
runsum2 = runsum2 + S[m]
ydot[B[m]] = a*K*S[m]-(d+k+r1)*KS[m]
for i in range(0,N/2-1):
ydot[G[i]] = a*P*S[i+1]-(d+k+r1)*PS[i]
for p in range(1,N/2):
ydot[p] = -S[p]*(r1+a*K+a*P)+k*KS[p-1]+d*(PS[p-1]+KS[p])
ydot[0] = Q-(r1+a*K)*S[0]+d*KS[0]+k*runsumPS
ydot[N/2] = k*KS[N/2-1]-(r2+a*P)*S[N/2]+d*PS[N/2-1]
ydot[G[N/2-1]] = a*P*S[N/2]-(d+k+r2)*PS[N/2-1]
ydot[3*N/2+1] = (d+k+r1)*runsumKS-a*K*runsum2
ydot[3*N/2+2] = (d+k+r1)*(runsumPS-PS[N/2-1])- \
a*P*runsum1+(d+k+r2)*PS[N/2-1]
ydot_new = []
for j in range(0,3*N/2+3):
ydot_new.extend(ydot[j])
return ydot_new
# Initial conditions
y0[0] = S10
for i in range(1,3*N/2+1):
y0[i] = 0
y0[3*N/2+1] = K0
y0[3*N/2+2] = P0
# Solve the DEs
soln = odeint(f,y0,time, mxstep = 5000)
for alpha in range(0,(N/2+1)):
S[alpha] = soln[:,alpha]
for beta in range((N/2)+1,N+1):
KS[beta-N/2-1] = soln[:,beta]
for gamma in range(N+1,3*N/2+1):
PS[gamma-N-1] = soln[:,gamma]
for alpha in range(0,(N/2+1)):
Splot[alpha][series] = soln[len1-1,alpha]
for beta in range((N/2)+1,N+1):
KSplot[beta-N/2-1][series] = soln[len1-1,beta]
for gamma in range(N+1,3*N/2+1):
PSplot[gamma-N-1][series] = soln[len1-1,gamma]
u1 = 0
u2 = 0
u3 = 0
for alpha in range(0,(N/2+1)):
u1 = u1 + Splot[alpha]
for beta in range((N/2)+1,N+1):
u2 = u2 + KSplot[beta-N/2-1]
for gamma in range(N+1,3*N/2+1):
u3 = u3 + PSplot[gamma-N-1]
K = soln[:,3*N/2+1]
P = soln[:,3*N/2+2]
Kplot[series] = soln[len1-1,3*N/2+1]
Pplot[series] = soln[len1-1,3*N/2+2]
utot = u1+u2+u3
#Plot
Kcrit = abs((Q/r2)*(1+epsilon)-utot)
v,i = Kcrit.min(0),Kcrit.argmin(0)
plt.plot(N,K00[i])
plt.show()
Thanks for any help.