I have simple code for traditional back-propagation (with the traditional sigmoid activation function) which is working fine.
Then I changed the sigmoid to the rectifier, and it fails to converge even for the simple XOR test.
I added "leakage" to the rectifier's derivative, and it still fails.
Network configuration:
[ input layer, 1 or 2 hidden layers, output layer ]
Input layer has no weights, it is just for accepting inputs.
All the hidden layers and the output layer have the same activation function (which used to be the sigmoid, now changed to be the rectifier).
The rectifier is:
f(x) = max(0,x)
f'(x) = sign(x)
which fails to make the network converge, so I added leakage, but it still fails.
The result of back-prop with traditional sigmoid
(network config is [2,8,1]):

The best result of my back-prop with rectified units (network config is [2,8,8,1]):
but I have obtained correct results only twice, after tens of trials.
Typically, it fails like this (network config is [2,8,8,1]):
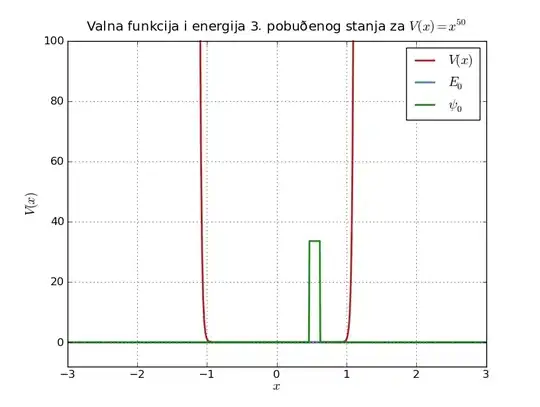
Or this (network config is [2,8,8,1]):
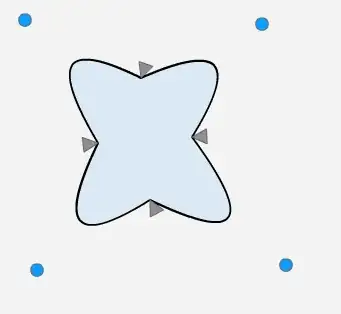
If I use 2 layers ([2,8,1]) it got stuck like this:

The network seems unable to get out of these local minima.
The code is here:
https://github.com/Cybernetic1/genifer5-c/blob/master/back-prop.c
Notice that there are 2 versions: one with traditional sigmoid and the other with _ReLU suffix.
My question is similar to this one: Neural network backpropagation with RELU but even in that question the answers are unsatisfactory and inconclusive.