The closest thing I've found to help explain what I need is here in this question: Draw equidistant points on a spiral
However, that's not exactly what I want.
The spiral to draw is an archimedean spiral and the points obtained must be equidistant from each other. (Quote: From the question linked above.)
This is precisely what I want given the Archimedean Spiral equation,  .
.
There is a specific set of data a user can input, they are NOT based on spirals but circular figures in general. They are as follows: center point [X,Y,Z], radius, horizontal separation [can be called X separation, depends on figure], and vertical separation [can be called Y separation, depends on figure], and most importantly degrees of rotation. I'd like the horizontal separation to be the distance between consecutive points since they are the ones that need to be the same distance between each other. I'd also like vertical separation to be the distance between the 'parallel' curves.
So given that specific input selection (and yes, some can be ignored), how can I iterate through all of the consecutive, equidistant points it would take to reach the input degrees (which can be very large but is finite) and return the X and Y point of each point of those points?
Basically what I'm try to achieve is a loop from zero to the number of degrees in the input, given all of the rest of the input and my preferences noted above, and drawing a point for all of the equidistant, consecutive points (if you decide to represent using code, just represent the drawing using a 'print').
I'm having a hard time explaining, but I think I got it pretty much covered. The points on this graph are exactly what I need:
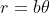 . Successive lines are then
. Successive lines are then  apart, so to obtain a 'vertical spacing' of
apart, so to obtain a 'vertical spacing' of  , set
, set 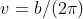 .
. . Rearranging,
. Rearranging, 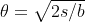 , allowing us to determine what angles correspond to the desired 'horizontal spacing'. If this approximation is not good enough, I would look at using something like Newton-Raphson. The question you link to uses also uses an approximation, although not the same one.
, allowing us to determine what angles correspond to the desired 'horizontal spacing'. If this approximation is not good enough, I would look at using something like Newton-Raphson. The question you link to uses also uses an approximation, although not the same one. ;
;  .
.