Let's look at the definition you posted for f(n) in O(g(n)):
f(n) = O(g(n)) means c · g(n) is an upper bound on f(n). Thus there
exists some constant c such that f(n) is always ≤ c · g(n), for
large enough n (i.e. , n ≥ n0 for some constant n0).
So, we only need to find one set of constants (c, n0) that fulfils
f(n) < c · g(n), for all n > n0, (+)
but this set is not unique. I.e., the problem of finding the constants (c, n0) such that (+) holds is degenerate. In fact, if any such pair of constants exists, there will exist an infinite amount of different such pairs.
Note that here I've switched to strict inequalities, which is really only a matter of taste, but I prefer this latter convention. Now, we can re-state the Big-O definition in possibly more easy-to-understand terms:
... we can say that f(n) is O(g(n)) if we can find a constant c such
that f(n) is less than c·g(n) or all n larger than n0, i.e., for all
n>n0.
Now, let's look at your function f(n)
f(n) = 3n^2 - 100n + 6 (*)
Let's describe your functions as a sum of it's highest term and another functions
f(n) = 3n^2 + h(n) (**)
h(n) = 6 - 100n (***)
We now study the behaviour of h(n) and f(n), respectively:
h(n) = 6 - 100n
what can we say about this expression?
=> if n > 6/100, then h(n) < 0, since 6 - 100*(6/100) = 0
=> h(n) < 0, given n > 6/100 (i)
f(n) = 3n^2 + h(n)
what can we say about this expression, given (i)?
=> if n > 6/100, the f(n) = 3n^2 + h(n) < 3n^2
=> f(n) < c*n^2, with c=3, given n > 6/100 (ii)
Ok!
- From (ii) we can choose constant c=3, given that we choose the other constant n0 as larger than 6/100. Lets choose the first integer that fulfils this: n0=1.
Hence, we've shown that (+) golds for constant set **(c,n0) = (3,1), and subsequently, f(n) is in O(n^2).
For a reference on asymptotic behaviour, see e.g.
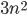 and
and 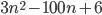 have the same asymptotic complexity.
have the same asymptotic complexity.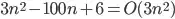
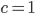
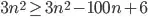
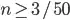
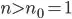 the inequality is always satisfied.
the inequality is always satisfied.
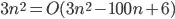

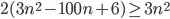
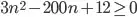
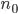 after which the inequality is always satisfied.
after which the inequality is always satisfied.