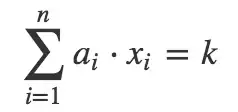3

I'm looking for an efficient solution to a specific case of integer factorization. By efficient I mean considerably faster than O(2^n), which I currently have (n represents the number of elements in the array after we are done).

Suppose we have the following array: [4, 5, 11] and a "goal" of 84.

We want to find out if it's possible to satisfy 4*a + 5*b + 11*c = 84,

given the following constraints:

  • 0 <= a <= 3
  • 0 <= b <= 2
  • 0 <= c <= 1

If we don't find a solution, we add an integer to the array, let's say 15: [4, 5, 11, 15]

Now we want to know if anything satisfies 4*a + 5*b + 11*c + 15*d = 84

given that

  • 0 <= a <= 4
  • 0 <= b <= 3
  • 0 <= c <= 2
  • 0 <= d <= 1

...and we repeat the process until we find a solution, or up to n times. I was wondering if we could exploit the repetitive properties of the problem to find an efficient solution:

  • The "goal" doesn't change
  • The integers come in ascending order
  • The max constraints for a,b,c... increase by 1 every time we add a new element
  • Every repeat something is added to the formula, but nothing is changed (other than the constraints)

Any ideas?

Salvador Dali
  • 214,103
  • 147
  • 703
  • 753
Atte Juvonen
  • 4,922
  • 7
  • 46
  • 89
  • 1
    When you have a solution for the first formula (with *a*, *b* & *c*), you can use the exact same solution for all other formulas, just set the remaining variables (*d*, *e*, etc...) to 0. – Amit Jan 07 '16 at 23:39
  • Oh, sorry if I used the wrong term. What should I call this? – Atte Juvonen Jan 07 '16 at 23:53
  • @Amit once we find a solution (at any step) we can stop the process. I'll edit this info into the question. – Atte Juvonen Jan 07 '16 at 23:54
  • 1
    If I am right, this problem belongs to the class of "integer linear programming" which is known to be NP-hard. So there is no hope to find a fast (polynomial) solution. –  Jan 08 '16 at 09:32

1 Answers1

3

First of all the term is wrong. It is not integer factorization, but rather a linear diophantine equation with many variables with some additional constrains.

Without your constrains it would be an easy task. Just find GCD(list of coefficients) and if it divides the free term - you have a solution, otherwise it does not.

With your constrains it can be a first step, but here if you see that there are solutions, they might not satisfy constrains.

I do not see a quick (polynomial solution) so here is how I would address it. You have enter image description here

I would use meet in the middle approach and would divide the equation with constrains in two parts:

Part 1 is enter image description here,

Part 2 is enter image description here

where I would divide them so that the number of computations performed in both parts would be approximately the same (taking into account constraints).

Now you iterate over the the first part and store everything in the dictionary. Then iterate over the second one and and check if the answer exists in the dictionary. If yes, you found a solution.

This divides exponent by 2 but requires memory.

This math answer may help someone to come up with a better approach that I was not able to find.

Community
  • 1
  • 1
Salvador Dali
  • 214,103
  • 147
  • 703
  • 753
  • 1
    The math answer you give contains an extremely useful insight, which allows for `O(1)` determination of no-solution in some cases. Since it has to be that `GCD(list of coefficients) divides k` and that the terms are increasing. This means that `k` has to be less than or equal to the first term (which is the smallest) for a solution to exist *at all*. This means that no solution will exist regardless of additional terms for the OPs example of `4*a + ... = 84`. Here, the GCD must be between `1 and 4 (inclusive)`, but that's too low for it to be divisible by `84`. – Nuclearman Jan 08 '16 at 03:42
  • @Nuclearman a,b,c... can be zero, so additional terms may turn up a solution. So for example, `4*0 + 5*0 + ... + 84*1 = 84` – Atte Juvonen Jan 08 '16 at 12:46
  • I'm having trouble understanding how to apply GCD here. For example, if the equation was `3a + 8b = 10`, the GCD of 3 and 8 would be 1, which divides 10, implying a solution when there is none. Am I doing something wrong? – Atte Juvonen Jan 08 '16 at 12:51
  • @AtteJuvonen: You mixed up the definition of divides. in your example, `GCD(3,8) / 10 = 0.1`, 0.1 is not an integer, so 1 does not divide 10.I will admit though that with zero an option, what I said really only means that you can quickly eliminate (set coefficient to 0, and leave it there) any term lower than the goal. So in your example, it is only at `84x = 84` that you need to even start testing coefficients. Also, if you consider just `3 / 10 = 0.3 and 8/10 = 0.8`, both are not integers. So they can be ignored in this case. – Nuclearman Jan 08 '16 at 17:15