Open quantum system modelling

Question

I have been working for a long time now on modelling an open quantum system using the Lindblad Equation. The Hamiltonian is the following:

However, two other matrices are added to the Hamiltonian. One of them has all the diagonal terms equal to -33.3333i and everything else zero. Another is a matrix with the third diagonal term equaling -0.033333i.

The Lindblad Equation is this:

where L_i are matrices (in the list: [L1,L2,L3,L4,L5,L6,L7]). The matrix for L_i is simply a 7x7 matrix with all zeros except L_(ii)=1. H is the total Hamiltonian, $\rho$ is the density matrix, and $\gamma$ is a constant equal to $2\pi kT/\hbar*E_{R}/(\hbar\omega_{c})$ where T is the temperature, k is the Boltzmann constant, and $\hbar$ = $h/2\pi$ , where h is Planck's constant. (Note that gamma is in natural units)

The following codes solves the Lindblad Equation, therefore calculating the density matrix. It then calculates and plots this versus time:

This is known as the site 3 population. is called a bra and is called a ket. Both are vectors. See the code for their definition in this case.

Here is the code:

from qutip import Qobj, Options, mesolve
import numpy as np
import scipy
from math import *
import matplotlib.pyplot as plt

hamiltonian = np.array([
    [215, -104.1, 5.1, -4.3, 4.7, -15.1, -7.8],
    [-104.1, 220.0, 32.6, 7.1, 5.4, 8.3, 0.8],
    [5.1, 32.6, 0.0, -46.8, 1.0, -8.1, 5.1],
    [-4.3, 7.1, -46.8, 125.0, -70.7, -14.7, -61.5],
    [4.7, 5.4, 1.0, -70.7, 450.0, 89.7, -2.5],
    [-15.1, 8.3, -8.1, -14.7, 89.7, 330.0, 32.7],
    [-7.8, 0.8, 5.1, -61.5, -2.5, 32.7, 280.0]
])

recomb = np.zeros((7, 7), dtype=complex)
np.fill_diagonal(recomb, 33.33333333)
recomb = recomb * -1j
trap = np.zeros((7, 7), complex)
trap[2][2] = -0.033333333333j
hamiltonian = recomb + trap + hamiltonian
H = Qobj(hamiltonian)

# Note the extra .0 on the end to convert to float
gamma = (2 * pi) * (296 * 0.695) * (35.0 / 150)

L1 = np.array([
    [1, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0]
])

L2 = np.array([
    [0, 0, 0, 0, 0, 0, 0], [0, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0]
])

L3 = np.array([
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 1, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0]
])      

L4 = np.array([
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0]
])

L5 = np.array([
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0]
])

L6 = np.array([
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 1, 0],
    [0, 0, 0, 0, 0, 0, 0]
])

L7 = np.array([
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 1]
])

# Since our gamma variable cannot be directly applied onto
# the Lindblad operator, we must multiply it with
# the collapse operators:  

rho0=Qobj(L1)

L1 = Qobj(gamma * L1)
L2 = Qobj(gamma * L2)
L3 = Qobj(gamma * L3)
L4 = Qobj(gamma * L4)
L5 = Qobj(gamma * L5)
L6 = Qobj(gamma * L6)
L7 = Qobj(gamma * L7)

options = Options(nsteps=1000000, atol=1e-5)

bra3 = [[0, 0, 1, 0, 0, 0, 0]]
bra3q = Qobj(bra3)

ket3 = [[0], [0], [1], [0], [0], [0], [0]]
ket3q = Qobj(ket3)

starttime = 0
# this is effectively just a label - `mesolve` alwasys starts from `rho0` -
# it's just saying what we're going to call the time at t0
endtime = 100
# Arbitrary - this solves with the options above
# (max 1 million iterations to converge - tolerance 1e-10)
num_intermediate_state = 100

state_evaluation_times = np.linspace(
    starttime,
    endtime,
    num_intermediate_state
)

result = mesolve(
    H,
    rho0,
    state_evaluation_times,
    [L1, L2, L3, L4, L5, L6, L7],
    [],
    options=options
)

number_of_interest = bra3q * (result.states * ket3q)

points_to_plot = []
for number in number_of_interest:
    if number == number_of_interest[0]:
        points_to_plot.append(0)
    else:
        points_to_plot.append(number.data.data.real[0])

plt.plot(state_evaluation_times, points_to_plot)
plt.show()
exit()

This code uses a Python module known as qutip. It has a builtin Lindblad Equation solver using scipy.integrate.odeint.

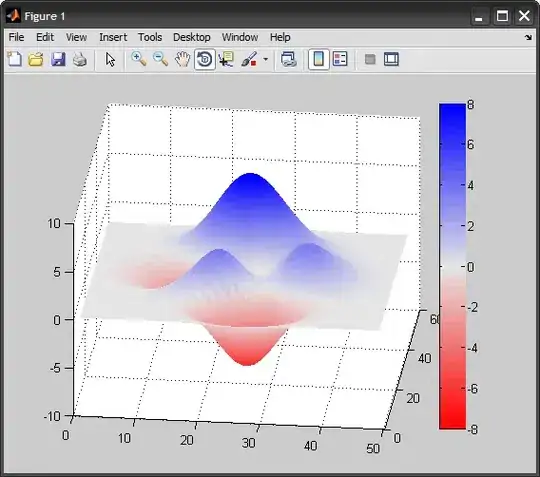
Currently, this program displays this:

However, the limit of the site 3 population is supposed to be 0. Therefore, it should decrease slowly down to zero. Especially by t=75, the decrease should start.

This code runs, but does not produce the correct result as I explained. So now, why doesn't it produce the right result? Is something wrong with my code?

I have looked at my code, each line to see if it matches up with the model I am using. They match up perfectly. The issue must be in the code, not the physics.

I have done some debug prompts, and all the matrices and the gamma is correct. I still, however, suspect something in the trap matrix. The reason I think so is because the plot looks like the dynamics of the system without the trap matrix, Could there be something wrong with the definition of the trap matrix that I am not noticing?

Note, the code takes a few minutes to run. Be patient while running the code!

"*Note, the code takes a few hours to run. Be patient while running the code!*" - I'm not sure many people will run code that takes more than a few seconds (minutes maybe) to answer a question. Have you tried stepping through it with a debugger to see if every line of code does what you expect it to? — Wai Ha Lee, Jan 08 '16 at 09:03
@WaiHaLee most of it goes on in the Lindblad Equation solver which is pretty hard to follow through. — TanMath, Jan 08 '16 at 09:05
A question being complicated to answer or taking a long time to run does not make it too broad, just hard to answer. But being hard to answer isn't off topic and the question shouldn't be closed. — SuperBiasedMan, Jan 14 '16 at 10:14
I think you would find a much more receptive crowd on the Physics Stack Exchange. There are more people there that can deal with Python than there are people here that can deal with QM. — Mike Wise, Jan 16 '16 at 14:18
@MikeWise fixing code is definitely off-topic for Physics.SE. — TanMath, Jan 16 '16 at 21:06
@TanMath I agree with you. I won't answer the question directly but I have significant experience debugging horrific physics models. I would strongly recommend implementing several simple test models. The mistake you have made here is going for the golden goose of getting it all to work in one swift move. This is a high risk strategy that assumes you will make no mistakes or at the very least you will be able to identify all of them. Test loads of trivial things e.g. identity matrices etc. These will probably pick up your error. Going straight for a complicated set of linear equations is nuts — Alexander McFarlane, Apr 12 '16 at 07:50

score 7 · Answer 1 · answered Apr 15 '16 at 12:51

(NB: this is an answer I hope in the programming sense, but not a physics answer.)

I ran your simulations independently, not using qutip, and I get essentially the same results. So the good news (maybe? :)) is that it's not an issue with your programming but a physics problem or at least a "choosing parameters" problem. Here are my results:

And a notebook with my working, the parameters are all the same as yours, apart from a different time-scale (explained below). I am using the same integration method asqutip but not qutip itself: Notebook Link.

A few notes:

When you perform from math import * you import a function gamma, and then you name a variable gamma, this caused problems for me and you might want to be careful about that in future.
When you multiply your linblad operators by \gamma rather than the sum they will appear twice in the master equation, so you are really specifying \gamma^2 here. This affects the time-scale.
<3|rho(t)|3> is just the third diagonal matrix element, you don't really need an inner product here.

A few things to check on the physics / parameter side.

From the paper you linked,
- is \Gamma definitely 100/3?
- is \kappa_3 definitely 0.1/3 and all others 0?
- is the initial state definitely all population in 0 state?
I am not up to date with energy transfer models but the hamiltonian here is non-hermitian and non-trivial imaginary parts (though still small) are generated on the density matrices diagonal. Make sure you understand exactly how and why these guys are using this model as it seems odd to me!

Open quantum system modelling

1 Answers1

A few notes:

A few things to check on the physics / parameter side.