Question 1:
... not sure .. how exactly deep and shallow history works?
Answer 1:
Note this:
A shallow history is indicated by a small circle containing an "H". It applies to the state region that directly encloses it.
Shallow history pseudostate represents the most recent active substate of its containing state (but not the substates of that substate). ...
Source: http://www.uml-diagrams.org/state-machine-diagrams.html#shallow-history-pseudostate
Question 2:
... I'm not sure if I always should start from initial point, which is outside of all composites?
Answer 2:
Yes. You start from the Initial Pseudostate of the root state (A in this case).
Example:
For the given state-chart and event chain, you would get the following result (simulated with Rhapsody):
after default transition to A
- value of x (transition to A):
x = 3
- value of x (entry A):
x = x * 2 = 6
- new state: A
after default transition to A::B
- new state: A::B
- value of x:
x = 6

after e1
- value of x (entry A::C):
x = x + 1 = 7
- new state: A::C
after default transition to A::C::G
- value of x (entry A::C::G):
x = x + 1 = 8
- new state: A::C::G

after e3
- value of x (exit A::C::G):
x = x - 2 = 6
- value of x (entry A::C::H):
x = x / 2 = 3
- new state: A::C::H
after e4
- value of x (entry A::C::G):
x = x + 1 = 4
- new state: A::C::G
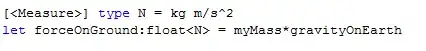
after e6
- value of x (exit A::C::G):
x = x - 2 = 2
- value of x (exit A::C):
x = x - 1 = 1
- value of x (exit A):
x = x - 1 = 0
- value of x (transition to Y):
x = (x * 4) + 2 = 2
- new state: Y

after e7
- value of x (entry A::C see the note above):
x = x + 1 = 3
- value of x (entry A::C::G):
x = x + 1 = 4
- new state: A::C::G
e4 is discarded