Modelling a Pendulum in C

Question

This is my code for attempting a while Loop to model a pendulum swing, however the values produced don't seem to help me:

#include <stdio.h>
#include <math.h>
#define PI 3.14159265

main()
{
    float theta = 0;   // initial value for angle
    float omega = 0.2; // initial value for angular speed
    float time = 0;    // initial time
    float dt = 0.01;   // time step

    while (theta < 2 * PI && -2*PI) {
        time = time + dt;
        theta = theta + omega*dt;

        printf("theta=%i, omega=%i, time=%i, and dt=%i\n", theta, omega, time, dt);
    }
    system("PAUSE");
}

How can I modify this to be more helpful? The while condition I have to use is that it should stop when the pendulum has made one revelation either forwards or backwards (-2PI or 2PI). I need to use the formula 'omega=omega-(g/l)dtsin(theta)' and NOT make the assumption that theta approximately equals sin(theta).

Answer 1

1. while(theta <2*PI&&-2*PI)

   In c if we want to combine multiple expressions we can combine them using logical operators as

   while((theta < 2 * PI) && (theta > -2 * PI))  
   

   PS- I am no physics expert. Change conditions as per your requirement

Answer 2

There are some problem in this code :

1. According to the standard you shouldn't use

   main()
   

   But either

   1. int main()
   2. int main(void)
   3. int main(int argc, char *argv[])

   Also don't forget

   return 0;
   

   Sample program :

   #include <stdio.h>
   
   int main(void) {       
       /* Do stuff */        
       return 0;    
   }
   

   If you wish to read more information about that, click here.

2. As LutzL pointed out you should use M_PI instead of your definition of PI. Just #include <math.h>

   That's how you would print the value for example :

   printf("\nValue of M_PI is %f\n\n", M_PI);
   

   Read more here.

3. As pointed out by rootkea :

   In c if we want to combine multiple expressions we can combine them using logical operators as

   while((theta < 2 * PI) && (theta > -2 * PI))

4. If you want greater precision (I think that this is the case) you should use double instead of float.

5. You are trying to print float variables with the "%i" format specifier. That's wrong, "%i" is used to print int signed integer and using the wrong specifier invokes undefined behavior. You should use "%f" to print float or double signed decimal.

Have a read about printf format specifiers here.

Answer 3

The angle equation that you use is not right. According to your expression it changes linearly with time, although the equation is harmonic:

        θ = θ₀cos(ωt)

where ω = g/L, L is the length of the pendulum and g the acceleration due to gravity.

Where thetaMax is the max deflection angle, g is gravity const, L is length of pendulum and t is time. So, you want to know thetaMaxfrom energy conservation law, for example.

Alrught, let's revise energy conservation law here:

As you know Potential energy at max deflection equals Kinetic energy at the lowest point of the pendulum path:

KE = ПE
m*g*L*sin(thetaMax) = m*sqr(omega)*sqr(L)/2

Approximately, for small angles:

m*g*L*thetaMax = m*sqr(omega)*sqr(L)/2
thetaMax = sqr(omega)*L/(2*g)

that is it. Here is code that calculates this type of oscillatory motion. All absolute values:

#include <stdio.h>
#include <math.h>
#define PI 3.14159265
#define L 1 //length of the pendulum
#define g 9.8  //gravity const

int main()
{
    double theta = 0; // initial value for angle
    double omega = 0.2; // initial value for angular speed
    double time = 0; // initial time
    double dt = 0.01; // time step

    double thetaMax = omega*omega*L/(2*g);

    while (theta < thetaMax) {
        time = time + dt;
        theta = thetaMax * sin(omega*time);
        printf("theta=%f, omega=%f, time=%f, and thetaMax=%f\n", theta, omega, time, thetaMax);
     }
    return 0;
}

It is going to calculate these parameters infinitely, so just limit theta in the condition of the while-loop to a desired angle of deflection.

Answer 4

The equation for a (simple, point mass on string) physical pendulum is

θ'' + k·sin(θ) = 0

where the constant:

k = g / L

contains gravitational g and length L.

θ is the angle measured from the position of rest, which of course is pointing down, that is, in a Cartesian coordinate system with the usual angle convention, at -90°. Thus the pendulum oscillations translate to theta oscillations around zero.

You could solve that (conservative) differential equation using symplectic Euler or Verlet/Leapfrog. Symplectic Euler in one variant has the loop (using ω=θ', that is, (θ',ω')=(ω, -k·sin(θ))

for(...) {
    omega -= k*sin(theta) * dt;
    theta  += omega * dt;
    t += dt;
    printf(...);
}

Answer 5

The idea of modelling, in simple terms, involves finding a mathematical representation of a physical phenomenon. In other words you need to "find" an equation that represents all the observable properties of the object in context, in your case a pendulum¹.

All you need to describe a pendulum is its equation of motion. To find it you firstly try to qualify the motion, by observing it:

If you try to displace it (many times with a very small angle) from its equilibrium point, you will mostly observe few swings, along the same path, where its amplitude decreases and it is brought back to its stable equilibrium, as if by some kind of restoring force, in other words the pendulum performs regular and repeating motion, called periodic motion

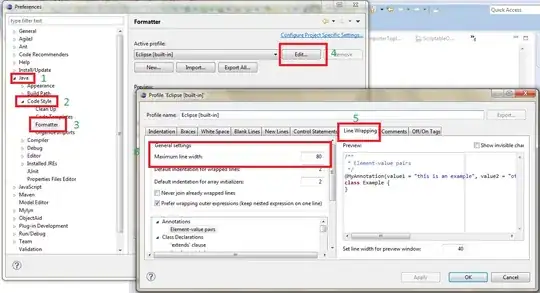
Thus, you are looking for a mathematical function that can represent a periodic motion, as it turns out a great candidate for this role are the trigonometric functions: sin and cos, that have the needed property i.e. repeat themselves with a period T.

To find and quantify this restoring force you use Newton's Second Law, where after you express everything in terms of the very small angle theta << 1 (that allows using of the small-angle approximation: sin(theta) = theta) of displacement theta, you get the wanted equation of motion, which is represented by the following differential equation:

with a great surprise (and to the first order of approximation), when you solve the above equation you find:

which approximately² matches the predictions from your observations (with some random error (standard deviation), preferably not systematic), i.e. the motion of the pendulum is described by the cosine function, it has periodic motion with an amplitude equal to the initial displacement and a period equal to:

and here is the catch,

the above equation for theta describes a pendulum that does not lose energy and its values repeat infinitely and that is why the loop in your program is an infinite loop harmonically oscillating ^{pun intended} with the same values!

If you want to observe a motion that slowly stops you need to add an additional damping force that will slowly subtract energy from the system. This damping force is represented by the following additional term in the equation of motion:

that again, can be expressed in terms of the angle theta. Now, when you solve the equation of motion, the amplitude gets multiplied by:

where b is the damping constant from which it depends how fast the motion will stop.

As a consequence of the above,

if you want to see something similar to the real pendulum you need to include this last exponential to your equation.

To do this just follow the great explanation offered by @Petr Stepanov, modifying thetaMax to include the above exponent.

#include <stdio.h>
#include <math.h>
#define PI 3.14159
#define E 2.71828      // Euler's number
#define L 1            // length of the pendulum
#define g  9.80665     // gravity const

int main() {

    double theta = 0.0; // initial value for angle
    double omega = 0.2; // initial value for angular speed
    double time = 0.0;  // initial time
    double dt = 0.01;   // time step
    double b = 0.5;     // modified damping constant

    double thetaMax = omega * omega * L / (2 * g);

    while (theta < thetaMax) {
        time = time + dt;
        theta = thetaMax * ldexp(E, (-b) * time) * sin(omega * time);

        printf("Deflection angle=%f, Angular frequency=%f, Time=%f\n", theta, omega, time);
    }

    return 0;
}

---

^{1. An object with mass m, hung on a fixed point with a non-elastic, "massless" thread with length l , that allows it to swing freely in a gravitational field, quantified by the gravitational acceleration constant g.}

^{2. It should be noted that: "all models are wrong; the practical question is how wrong do they have to be to not be useful"}