2D Elastic Ball Collision Physics

Question

I am making a program that involves elastic ball physics. I have worked out all of the maths for collision against walls and stationary objects, but I cannot figure out what happens when two moving balls collide. I have mass and velocity (x and y velocity to be exact, but velocity of each ball and their direction will do) and would like the formulae for those. Remember - this is a perfectly elastic collision - so no spinning balls, etc.

Could you please clarify what kind of formula are you looking for? What do you already have, and what is missing. — Robert Bräutigam, Feb 04 '16 at 20:42
Possible duplicate of [JAVA elastic collision of moving and non moving circles](http://stackoverflow.com/questions/23180453/java-elastic-collision-of-moving-and-non-moving-circles) — Lutz Lehmann, Feb 04 '16 at 23:14
Other questions on the same topic: https://stackoverflow.com/q/29382782/3088138 and https://stackoverflow.com/q/28122594/3088138. — Lutz Lehmann, Feb 04 '16 at 23:16

cromod · Answer 1 · 2016-11-18T20:58:33.463

This wikipedia article provides a formula to compute velocities after collision between two particles :

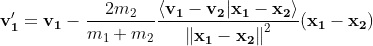
$\mathbf{v'_1}=\mathbf{v_1}-\frac{2m_2}{m_1+m_2}\frac{\left \langle \mathbf{v_1}-\mathbf{v_2}| \mathbf{x_1}-\mathbf{x_2}\right \rangle }{{\left \| \mathbf{x_1}-\mathbf{x_2} \right \|}^{2}} (\mathbf{x_1}-\mathbf{x_2})$

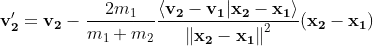
$\mathbf{v'_2}=\mathbf{v_2}-\frac{2m_1}{m_1+m_2}\frac{\left \langle \mathbf{v_2}-\mathbf{v_1}| \mathbf{x_2}-\mathbf{x_1}\right \rangle }{{\left \| \mathbf{x_2}-\mathbf{x_1} \right \|}^{2}} (\mathbf{x_2}-\mathbf{x_1})$

There are many reasons to use this formula :

you just need the velocity vectors of your balls before collision, their mass and their position,
you don't need to define angles of deviation,
the operations are simple (just dot product required),
the vectors can be expressed in any coordinates system.

There is no proof in the wikipedia article so I provide it below.

Definition of the problem

For each ball we define :

mi the mass
vi the vector of velocity before collision
v'i the vector of velocity after collision
Oi the point of center
xi the vector of Oi position

The unit vector n is normal to the surfaces of balls at the point of contact.

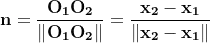
$\mathbf{n}=\frac{\mathbf{O_1O_2}}{\left \| \mathbf{O_1O_2}\right \|}=\frac{\mathbf{x_2 - x_1}}{\left \| \mathbf{x_2 - x_1}\right \|}$

The unit vector t is tangent to the surfaces of balls at the point of contact.

Physics law to use

The conservation of the total momentum is expressed by :

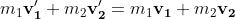
$m_1\mathbf{v'_1}+m_2\mathbf{v'_2}=m_1\mathbf{v_1}+m_2\mathbf{v_2}$

The conservation of total kinetic energy is expressed by :

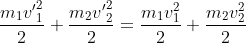
$\frac{m_1 {v'}_1^{2}}{2}+\frac{m_2 {v'}_2^{2}}{2}=\frac{m_1 v_1^{2}}{2}+\frac{m_2 v_2^{2}}{2}$

As there is no force applied in the tangential direction, the tangential components of velocities are unchanged after collision :

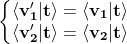
$\left\{\begin{matrix} \left \langle \mathbf{v'_1}|\mathbf{t} \right \rangle=\left \langle \mathbf{v_1}|\mathbf{t} \right \rangle \\ \left \langle \mathbf{v'_2}|\mathbf{t} \right \rangle=\left \langle \mathbf{v_2}|\mathbf{t} \right \rangle \end{matrix}\right.$

Proof

The tangential components of velocities are unchanged. So we can rewrite the conservation laws with normal components and we have a 1D problem now :

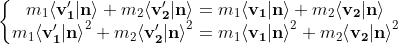
$\left\{\begin{matrix} m_1 {\left \langle \mathbf{v'_1}|\mathbf{n} \right \rangle}+m_2 {\left \langle \mathbf{v'_2}|\mathbf{n} \right \rangle} =m_1 {\left \langle \mathbf{v_1}|\mathbf{n} \right \rangle}+m_2 {\left \langle \mathbf{v_2}|\mathbf{n} \right \rangle} \\ m_1 {\left \langle \mathbf{v'_1}|\mathbf{n} \right \rangle}^{2}+m_2 {\left \langle \mathbf{v'_2}|\mathbf{n} \right \rangle}^{2}=m_1 {\left \langle \mathbf{v_1}|\mathbf{n} \right \rangle}^{2}+m_2 {\left \langle \mathbf{v_2}|\mathbf{n} \right \rangle}^{2} \end{matrix}\right.$

The conservation of kinetic energy can be factorized then simplified with the conservation of momentum :

$m_1 {\left \langle \mathbf{v'_1}|\mathbf{n} \right \rangle}^{2}-m_1 {\left \langle \mathbf{v_1}|\mathbf{n} \right \rangle}^{2}=m_2 {\left \langle \mathbf{v_2}|\mathbf{n} \right \rangle}^{2}-m_2 {\left \langle \mathbf{v'_2}|\mathbf{n} \right \rangle}^{2}$

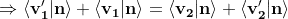
$\Rightarrow {\left \langle \mathbf{v'_1}|\mathbf{n} \right \rangle}+{\left \langle \mathbf{v_1}|\mathbf{n} \right \rangle}={\left \langle \mathbf{v_2}|\mathbf{n} \right \rangle}+{\left \langle \mathbf{v'_2}|\mathbf{n} \right \rangle}$

We combine this last expression with the conservation of momentum and we get the normal component of v'1 :

$\left \langle \mathbf{v'_1}| \mathbf{n}\right \rangle=\frac{(m_1-m_2)\left \langle \mathbf{v_1}| \mathbf{n}\right \rangle + 2 m_2\left \langle \mathbf{v_2}| \mathbf{n}\right \rangle}{m_1+m_2} =\left \langle \mathbf{v_1}| \mathbf{n}\right \rangle-\frac{ 2 m_2\left \langle \mathbf{v_1-v_2}| \mathbf{n}\right \rangle}{m_1+m_2}$

Finally, we find the formula of the wikipedia article for v'1 :

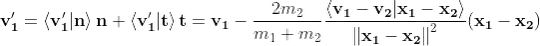
$\mathbf{v'_1}=\left \langle \mathbf{v'_1}| \mathbf{n}\right \rangle\mathbf{n}+\left \langle \mathbf{v'_1}| \mathbf{t}\right \rangle\mathbf{t}=\mathbf{v_1}-\frac{2m_2}{m_1+m_2}\frac{\left \langle \mathbf{v_1}-\mathbf{v_2}| \mathbf{x_1}-\mathbf{x_2}\right \rangle }{{\left \| \mathbf{x_1}-\mathbf{x_2} \right \|}^{2}} (\mathbf{x_1}-\mathbf{x_2})$

The formula of v'2 is symmetrical.

Related: https://stackoverflow.com/questions/345838/ball-to-ball-collision-detection-and-handling — sdgfsdh, Nov 08 '20 at 18:25
Clarification on the notation: The vertical pipe like `` simply means the dot product of `v1` and `n`. I haven't seen that notation before (wikipedia uses a comma), is that common? — theicfire, Dec 28 '22 at 01:44
@theicfire it is a common notation in quantum mechanics, and probably higher level classical mechanics as well. — Andrea B., Jan 09 '23 at 08:21

score 2 · Answer 2 · answered Jul 11 '20 at 19:08

Since I'm doing a remake on blobby, the the bodies are not necessarily balls - hit angles are not related to distance between X1,X2. So I was using the equations from this: https://williamecraver.wixsite.com/elastic-equations

below is the code that computes vector angle from dx dy velocities: Further below are the equations (that require the converted vector input). code is in python 3.8x. Tuples are input and output to the functions.

def angle_ofdxdy(dxdy):  # returns angle, z
  dx, dy = dxdy[0], dxdy[1]
  if abs(dy) < 0.01: #prevent div by zero
    dy = 0.01
  # https://math.stackexchange.com/questions/1327253/how-do-we-find-out-angle-from-x-y-coordinates
  z = (dx ** 2 + dy ** 2) ** 0.5
  angle = 2 * atan(dy / (dx + z))
  return (round(angle, 4), z)

below is a prep function that uses the above before calling the equations:

def calc_impulse_xy1xy2(xy1_xy2, ball_mass=1, wall_mass=10000000, gamma=0):
  xy1, xy2 = xy1_xy2
  a1, z = angle_ofdxdy(xy1)
  a2, z2 = angle_ofdxdy(xy2)
  # print(f'xy xy translator called for xy={xy1}, xy2{xy2}, angles {degrees(a1):.0f},  {degrees(a2):.0f}')
  return cv1v2(z, a1, z2, a2, ball_mass, wall_mass, gamma)

below are the actual equasions:

def cv1v2(ball_velocity=5, ball_theta=0, wall_velocity=0, wall_theta=0, ball_mass=1, wall_mass=10000000, gamma=0):
  g = gamma  # 0 needs further explainig. ba
  t1,t2 = ball_theta, wall_theta
  v1,v2 = ball_velocity, wall_velocity  # a scalar.
  m1,m2 = ball_mass, wall_mass

  # print('pi/2 is',pi/2)
  vx = (v1 * cos(t1 - g) * (m1 - m2) + 2 * m2 * v2 * cos(t2 - g)) * cos(g) / (m1 + m2) + v1 * sin(t1 - g) * cos(g + pi / 2)
  vy = (v1 * cos(t1 - g) * (m1 - m2) + 2 * m2 * v2 * cos(t2 - g)) * sin(g) / (m1 + m2) + v1 * sin(t1 - g) * sin(g + pi / 2)
  v2x = (v2 * cos(t2 - g) * (m2 - m1) + 2 * m1 * v1 * cos(t1 - g)) * cos(g) / (m1 + m2) + v2 * sin(t2 - g) * cos(g + pi / 2)
  v2y = (v2 * cos(t2 - g) * (m2 - m1) + 2 * m1 * v1 * cos(t1 - g)) * sin(g) / (m1 + m2) + v2 * sin(t2 - g) * sin(g + pi / 2)
  xyxy = ((round(vx, 2), round(vy, 2)), (round(v2x, 2), round(v2y, 2)))
  print(f'Ball: {v1:.1f}({degrees(t1):.0f}\u2070)\t Player:{v2:.1f}({degrees(t2):.0f}\u2070),  impact angle:{degrees(g):.0f}\u2070 masses:{m1},{m2} \nresult:{xyxy}')
  return xyxy

The function is referring to ball and wall. This is just a hint in case you want to test wall bouncing using the same equations (there's default heavy weight assigned to the second object). You can put identical masses of course in function call. Tested. Working

This approach assumes you calculated Gamma - the angle of contact. It is faily easy if you have full info of the collision point and shape of your objects. Especially if at least one is a ball

2D Elastic Ball Collision Physics

2 Answers2

Linked