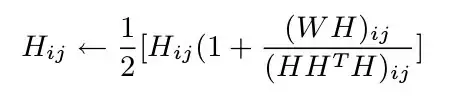Symmetric Non negative Matrix Factorization in R

Question

I am trying to implement NMF in R based on the following formula :
H is initially guess and then iteratively update based on this formula. I wrote this code but it takes like ever to execute. How can I rewrite this code? W is similarity matrix.

sym.nmf <- function ( W )
{
        N <- ncol(W)
        set.seed(1234)
        H <- matrix(runif(N * k, 0, 1),N,k)

        J1 <- 0

        while (0 < 1)
        {
                HT <- t(H)
                A <- W %*% H
                B <- H %*% HT %*% H
                H <- 0.5 * ( H * ( 1 + ( A / B )))
                J = W - (H %*% t(H))
                J = sum (J^2)
                if ( (J1 != 0 ) && (J > J1) )
                        return (H1)
                H1 <- H
                J1 <- J
        }

}

Answer 1

Here's a rework of the sym.nmf function with some statistically important improvements and speed gains along the way.

1. Add a relative tolerance (rel.tol) parameter to break the loop when J[i] is within rel.tol percent of J[i-1]. The way you have it set up, you will only stop the loop when 0 == 1 or machine precision becomes more variable than the fit itself. In theory, your function will never converge.

2. Add a seed, because reproducibility is important. Along this line, you may think of initializing with Non-negative double SVD to get a head start. However, depending on your application, this may drive your NMF into a local minima that is not representative of the global minima so it can be dangerous. In my case I get locked into a SVD-like minima and the NMF ends up converging at a state totally unlike the factorization from a random initialization.

3. Add a maximum number of iterations (max.iter), because sometimes you don't want to run a million iterations to reach your tolerance threshold.

4. Substitute in the crossprod and tcrossprod functions for the base %*% function. This nets about a 2x speed gain depending on matrix size.

5. Reduce the number of times convergence is checked, because calculating the residual signal in W after subtraction of HH^T takes nearly half of the computing time. You can assume it's going to take hundreds to thousands of iterations to converge, so just check for convergence every 100 cycles.

Updated function:

sym.nmf <- function (W, k, seed = 123, max.iter = 10000, rel.tol = 1e-10) {
  set.seed(seed)
  H <- matrix(runif(ncol(W) * k, 0, 1),ncol(W),k)
  J <- c()
  for(i in 1:max.iter){
    H <- 0.5*(H*(1+(crossprod(W,H)/tcrossprod(H,crossprod(H)))))

    # check for convergence every 100 iterations
    if(i %% 100 == 0){
      J <- c(J,sum((W - tcrossprod(H))^2))
      plot(J, xlab = "iteration", ylab = "total residual signal", log = 'y')
      cat("Iteration ",i,": J =",tail(J)[1],"\n")
      if(length(J) > 3 && (1 - tail(J, 1)/tail(J, 2)[1]) < rel.tol){
        return(H)
      }    
    }
    if(i == max.iter){
      warning("Max.iter was reached before convergence\n")
      return(H)
    }
  }
}

The objective function can be isolated as well, and Rfast can be used for parallelized computing of Rfast::Crossprod() and Rfast::Tcrossprod() as well.

sym.nmf <- function (W, k, seed = 123, max.iter = 100, rel.tol = 1e-10) {
  set.seed(seed)
  require(Rfast)
  H <- matrix(runif(ncol(W) * k, 0, 1),ncol(W),k)
  J <- c()
  for(i in 1:max.iter){
    H <- 0.5 * fit_H(W,H, num.iter = 100)
    J <- c(J,sum((W - tcrossprod(H))^2))
    plot(J, xlab = "iteration", ylab = "total residual signal", log = 'y')
    cat("Iteration ",i,": J =",tail(J, n = 1),"\n")
    if(length(J) > 3 && (1 - tail(J, 1)/tail(J, 2)[1]) < rel.tol){
      return(H)
    }
    if(i == max.iter){
      warning("Max.iter was reached before convergence\n")
      return(H)
    }
  }
}

fit_H <- function(W,H, num.iter){
  for(i in 1:num.iter){
    H <- 0.5*(H*(1+(Rfast::Crossprod(W,H)/Rfast::Tcrossprod(H,Rfast::Crossprod(H,H)))))
  }
  H
}

Now this objective function can be translated to Rcpp for further speed gains. Parallelization may also achieve further gains, either within the objective function (parallelized crossprod and tcrossprod) or by running multiple factorizations in parallel (since multiple restarts are often required to discover a robust solution).