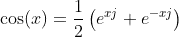You can try to use the definition of cosine based on the complex exponential:
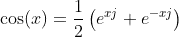
where j^2=-1.
Store exp((2 * PI*freqscale[currentcarrier] / fs)*j) and exp(phase*j). Evaluating cos(...) then resumes to a couple of products and additions in the for loops, and sin(), cos() and exp() are only called a couple of times.
Here goes the implementation:
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <complex.h>
#include <time.h>
#define PI 3.141592653589
typedef struct cos_plan{
double complex* expo;
int size;
}cos_plan;
double phase_func(double* calibdata, long size, double* freqscale, double fs, double phase, int currentcarrier){
double result=0; //initialization
for (int i = 0; i < size; i++){
result += calibdata[i] * cos ( (2 * PI*freqscale[currentcarrier] * i / fs) + (phase*(PI / 180.) - (PI / 2.)) );
//printf("i %d cos %g\n",i,cos ( (2 * PI*freqscale[currentcarrier] * i / fs) + (phase*(PI / 180.) - (PI / 2.)) ));
}
result = fabs(result / size);
return result;
}
double phase_func2(double* calibdata, long size, double* freqscale, double fs, double phase, int currentcarrier, cos_plan* plan){
//first, let's compute the exponentials:
//double complex phaseexp=cos(phase*(PI / 180.) - (PI / 2.))+sin(phase*(PI / 180.) - (PI / 2.))*I;
//double complex phaseexpm=conj(phaseexp);
double phasesin=sin(phase*(PI / 180.) - (PI / 2.));
double phasecos=cos(phase*(PI / 180.) - (PI / 2.));
if (plan->size<size){
double complex *tmp=realloc(plan->expo,size*sizeof(double complex));
if(tmp==NULL){fprintf(stderr,"realloc failed\n");exit(1);}
plan->expo=tmp;
plan->size=size;
}
plan->expo[0]=1;
//plan->expo[1]=exp(2 *I* PI*freqscale[currentcarrier]/fs);
plan->expo[1]=cos(2 * PI*freqscale[currentcarrier]/fs)+sin(2 * PI*freqscale[currentcarrier]/fs)*I;
//printf("%g %g\n",creall(plan->expo[1]),cimagl(plan->expo[1]));
for(int i=2;i<size;i++){
if(i%2==0){
plan->expo[i]=plan->expo[i/2]*plan->expo[i/2];
}else{
plan->expo[i]=plan->expo[i/2]*plan->expo[i/2+1];
}
}
//computing the result
double result=0; //initialization
for(int i=0;i<size;i++){
//double coss=0.5*creall(plan->expo[i]*phaseexp+conj(plan->expo[i])*phaseexpm);
double coss=creall(plan->expo[i])*phasecos-cimagl(plan->expo[i])*phasesin;
//printf("i %d cos %g\n",i,coss);
result+=calibdata[i] *coss;
}
result = fabs(result / size);
return result;
}
int main(){
//the parameters
long n=100000000;
double* calibdata=malloc(n*sizeof(double));
if(calibdata==NULL){fprintf(stderr,"malloc failed\n");exit(1);}
int freqnb=42;
double* freqscale=malloc(freqnb*sizeof(double));
if(freqscale==NULL){fprintf(stderr,"malloc failed\n");exit(1);}
for (int i = 0; i < freqnb; i++){
freqscale[i]=i*i*0.007+i;
}
double fs=n;
double phase=0.05;
//populate calibdata
for (int i = 0; i < n; i++){
calibdata[i]=i/((double)n);
calibdata[i]=calibdata[i]*calibdata[i]-calibdata[i]+0.007/(calibdata[i]+3.0);
}
//call to sample code
clock_t t;
t = clock();
double res=phase_func(calibdata,n, freqscale, fs, phase, 13);
t = clock() - t;
printf("first call got %g in %g seconds.\n",res,((float)t)/CLOCKS_PER_SEC);
//initialize
cos_plan plan;
plan.expo=malloc(n*sizeof(double complex));
plan.size=n;
t = clock();
res=phase_func2(calibdata,n, freqscale, fs, phase, 13,&plan);
t = clock() - t;
printf("second call got %g in %g seconds.\n",res,((float)t)/CLOCKS_PER_SEC);
//cleaning
free(plan.expo);
free(calibdata);
free(freqscale);
return 0;
}
Compile with gcc main.c -o main -std=c99 -lm -Wall -O3. Using the code you provided, it take 8 seconds with size=100000000 on my computer while the execution time of the proposed solution takes 1.5 seconds... It is not so impressive, but it is not negligeable.
The solution that is presented does not involve any call to cos of sin in the for loops. Indeed, there are only multiplications and additions. The bottleneck is either the memory bandwidth or the tests and access to memory in the exponentiation by squaring (most likely first issue, since i add to use an additional array of complex).
For complex number in c, see:
If the problem is memory bandwidth, then parallelism is required... and directly computing cos would be easier. Additional simplifications coud have be performed if freqscale[currentcarrier] / fs were an integer. Your problem is really close to the computation of Discrete Cosine Transform, the present trick is close to the Discrete Fourier Transform and the FFTW library is really good at computing these transforms.
Notice that the present code can produce innacurate results due to loss of significance : result can be much larger than cos(...)*calibdata[] when size is large. Using partial sums can resolve the issue.