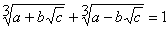How do I write this equation in Python?

Question

I really don't know how to write this correctly. This is how I tried:

def is_cardano_triplet(a, b, c):
    f = lambda x: x ** 1. / 2
    g = lambda x: x ** 1. / 3
    return g(a + b*f(c)) + g(a - b*f(c)) == 1

print is_cardano_triplet(2,1,5) # I should get True

I should get True for 2, 1, 5, but I'm not. What's wrong with my function?

Take a look at [Is floating point math broken?](http://stackoverflow.com/questions/588004/is-floating-point-math-broken) — Jeremy, Apr 19 '16 at 19:40
There is a `math.sqrt` or `math.pow` function, you don't need to implement your own. — OneCricketeer, Apr 19 '16 at 19:43
You'll need to reformulate your equation to work purely in terms of integers, or perhaps bring in a sufficiently powerful symbolic math library. (Also, `x ** 1. / 2` is `(x ** 1.) / 2`, not `x ** (1. / 2)`.) — user2357112, Apr 19 '16 at 19:44
Python follows [BEDMAS](http://mathcentral.uregina.ca/QQ/database/QQ.09.07/h/brit1.html) and as user2357112 has pointed out, you are not raising your numbers to a fractional power unless you implement brackets. — Tadhg McDonald-Jensen, Apr 19 '16 at 19:46
just found this, can help you: https://github.com/abusayeedomar/cardano-triplets-solution/blob/master/triplets.py — DevLounge, Apr 19 '16 at 20:08
@MarcoBonelli: Well, a program is meant to be heavily involved. It's just that you can't simply transcribe the formula for what you're supposed to calculate and expect the result to be a correct, efficient program. You need to apply some math and find a good algorithm. — user2357112, Apr 19 '16 at 20:57
@user2357112 the more I browse Project Euler, the more I convince myself about this, I see what you mean! — Marco Bonelli, Apr 19 '16 at 20:59

Marco Bonelli · Accepted Answer · 2018-11-04T16:54:32.230

7

Doing a few calculations, I found out that:

and therefore:

Now, due to floating point arithmetic being imprecise on binary-based systems for known reasons, the first formula is pretty hard to compute precisely. However, the second one is much easier to compute without floating point precision errors since that it doesn't involve irrational functions and a, b and c are integers.

Here's the smart solution:

def is_cardano_triplet(a, b, c):
    return (a + 1)**2 * (8*a - 1) - 27*b**2*c == 0

>>> is_cardano_triplet(2, 1, 5)
True

edited Nov 04 '18 at 16:54

answered Apr 19 '16 at 20:22

Marco Bonelli

63,369
21
118
128

Of course, to solve the Project Euler problem, generating triplets and *testing* whether they're Cardano triplets would still be unworkably inefficient. You might try iterating over possible values of `(a + 1) / 3` (as `a` must be congruent to 2 mod 3) and considering factors of `(a + 1) / 3` and square factors of `(8*a - 1) / 3` to generate valid `b` values, from which the corresponding `c` immediately follows. – user2357112 Apr 19 '16 at 21:12

score 1 · Answer 2 · edited Apr 19 '16 at 21:26

1

The power operator (**) has a higher priority than the division one (/). So you need to set parentheses:

f = lambda x: x ** (1./3)

Still, floating point operations are not exact, so you have to compare with some small uncertainty:

def is_cardano_triplet(a, b, c):
    f = lambda x: x ** (1. / 2)
    g = lambda x: x ** (1. / 3)
    return abs(g(a + b*f(c)) + g(a - b*f(c)) - 1) < 1e-10

Now you get the problem, that negative numbers are only allowed for roots of odd numbers, but floating points aren't exact, so you have to handle negative numbers by hand:

def is_cardano_triplet(a, b, c):
    f = lambda x: x ** (1. / 2)
    g = lambda x: (-1 if x<0 else 1) * abs(x) ** (1. / 3)
    return abs(g(a + b*f(c)) + g(a - b*f(c)) - 1) < 1e-10

Now

print is_cardano_triplet(2,1,5)

results in True.

edited Apr 19 '16 at 21:26

Marco Bonelli

63,369
21
118
128

answered Apr 19 '16 at 19:45

Daniel

42,087
4
55
81

while this is part of it, the function still returns False because of floating point rounding, see [Is floating point math broken?](http://stackoverflow.com/questions/588004/is-floating-point-math-broken). – Tadhg McDonald-Jensen Apr 19 '16 at 19:47
`print is_cardano_triplet(2,1,5)` gives: `ValueError: negative number cannot be raised to a fractional power` for me. – Fred Larson Apr 19 '16 at 19:52
2

Comparing with a tolerance will just produce *different* wrong results. You'll get false positives for inputs that aren't Cardano triplets. – user2357112 Apr 19 '16 at 19:52

How do I write this equation in Python?

2 Answers2