I would like to
- take a matrix of
global datawithlon/latvalues (e.g. surface air temperature), missing values are given asNAs. - plot it in an equal area or compromise (e.g. Robinson) projection (both tropical and polar regions should be represented)
- add an outline of the continents on top
- add a grid and labels on the side
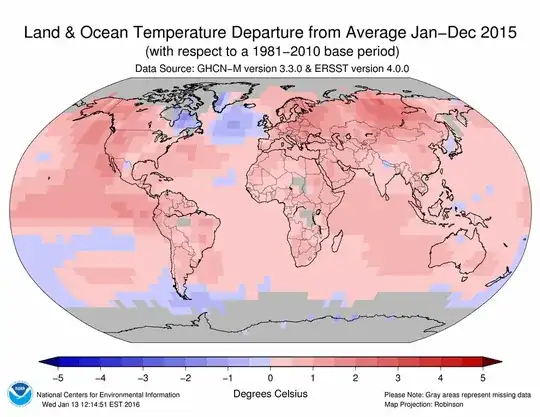
Edit: The projection I'm looking for looks something like this:
The basic plot with lat/lon values to get a rectangular image with map on top is straightforward, but once I try to project the matrix data things appear much more complicated. It can't really be this complicated - I must be missing something. Trying to understand openproj , spTransform and SpatialPoints gave me the impression I have to convert my matrix coordinates so that I have a sort of grid object.
The example below is based on the answer to R - Plotting netcdf climate data and uses the NOAA air surface temperature data from http://www.esrl.noaa.gov/psd/data/gridded/data.ncep.html.
Edit: There seem to be (at least) three ways to approach this, one using mapproj (and converting the matrix to polygons, as pointed out in the response below), another one using openproj, CRS and spTransform', and maybe a third one usingraster`.
library(ncdf)
library(fields)
temp.nc <- open.ncdf("~/Downloads/air.1999.nc")
temp <- get.var.ncdf(temp.nc,"air")
temp[temp=="32767"] <- NA # set missing values to NA
temp.nc$dim$lon$vals -> lon
temp.nc$dim$lat$vals -> lat
temp.nc$dim$time$vals -> time
temp.nc$dim$level$vals -> lev
lat <- rev(lat)
temp <- temp[, ncol(temp):1, , ] #lat being our dimension number 2
lon <- lon -180
temp11 <- temp[ , , 1, 1] #Level is the third dimension and time the fourth.
So the data is lon x lat x temp11 and can be plotted as an image
image.plot(lon,lat,temp11-273.15,horizontal=TRUE)
library(maptools)
map("world",add=TRUE,wrap=TRUE)
All is good up to here and works. But I want both the map and the image to be projected onto a more relevant grid. So what follows is my attempt to find a way to do this.
Trying to project the map using mapproj (fails)
library("mapproj")
eg<-expand.grid(lon,lat)
xyProj<-mapproject(eg[,1],eg[,2],projection="vandergrinten")
im<-as.image(temp11,x=xyProj$x,y=xyProj$y) # fails
image.plot(im)
Whereas this projects the continent outlines at least (but some of the lines get distorted)
map("world",proj="vandergrinten",fill=FALSE)
How can the two be combined? Thanks!