0

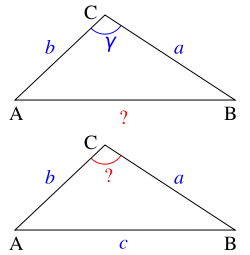
I'm working on a problem in c++ where I need to determine the angle between a line represented as 2 points in 3d (etc, x.y.z coordinates) and a disconnected point. Here are some pictures that might be easier to understand.

This is in 2D to display it easier

So what I need help with is finding this angle

With angle

I've been searching for several hours to solve this now, and I suspect that I've just missed something obvious. But if anyone can help me with this I will be very greatful:)

magnulef
  • 25
  • 3
  • suggest posting the picture directly rather than linking to imgurl – Jason S May 04 '16 at 03:44
  • 1
    Have you heard about math.stackexchange.com? That's there you wanna go. Example: http://math.stackexchange.com/questions/413482/angle-between-different-rays-3d-line-segments-and-computing-their-angular-rela and http://math.stackexchange.com/questions/463415/angle-between-two-3d-lines Here we discuss programming. – Support Ukraine May 04 '16 at 03:44
  • 1
    Computational geometry is a gray area between math and programming. Please get off your high horse. – Jason S May 04 '16 at 03:47

3 Answers3

2

You have 2 vectors, first related to line in 3D and other vector connecting end point of the line and a point in 3D.

To calculate angle theta between 2 vectors, you can take advantage of the fact that V1.V2 = |V1| x |V2| x consine(theta)

Here is code snippet I copied from here, to calculate dot product.

#include<numeric>    

int main() { 
    double V1[] = {1, 2, 3}; // vector direction i.e. point P2 - point P1
    double V2[] = {4, 5, 6}; // vector direction i.e. point P3 - point P2

    std::cout << "The scalar product is: " 
              << std::inner_product(begin(V1), end(V1), begin(V2), 0.0);

    // TODO: Get theta

    return 0;
}

Once you have the dot product, divide it by magnitudes of 2 vectors and then take inverse consine to get theta.

Community
  • 1
  • 1
vcp
  • 962
  • 7
  • 15
0

Use the Law of Cosines:

gamma = acos((asq + bsq - csq) / 2 / sqrt(asq*bsq))

where asq and bsq are the squared distances between the vertex and the other two points, and csq is the squared distance between those two points.

(drawing from Wikipedia)

Jason S
  • 184,598
  • 164
  • 608
  • 970
  • Why the downvote? This is exactly the approach to use. OP still needs to calculate `asq`, `bsq`, `csq` from the original coordinates, but that's fairly easy. – Jason S May 04 '16 at 03:42
-1

let say you have A(x1,y1,z1) B(x2,y2,z2) C(x3,y3,z3) and the common point is B. So the equation of the line AB becomes : (x1-x2)i + (y1-y2)j + (z1-z2)k and that for BC it is : (x2-x3)i + (y2-y3)j + (z2-z3)k

Cos theta = (AB.BC)/(|AB|*|BC|)

Here is the code

#include<iostream>
#include<math.h>
#define PI 3.14159265
using namespace std; 
int main()
{
    int x1,x2,x3,y1,y2,y3,z1,z2,z3;
    cout<<"for the first\n";
    cin>>x1>>y1>>z1;
    cout<<"\nfor the second\n";
    cin>>x2>>y2>>z2;
    cout<<"\nfor the third\n";
    cin>>x3>>y3>>z3;
    float dot_product = (x1-x2)*(x2-x3) + (y1-y2)*(y2-y3)+ (z1-z2)*(z2-z3);
    float mod_denom1 = sqrt((x1-x2)*(x1-x2) + (y1-y2)*(y1-y2) + (z1-z2)*(z1-z2));
    float mod_denom2 = sqrt((x2-x3)*(x2-x3) + (y2-y3)*(y2-y3) + (z2-z3)*(z2-z3));
    float cosnum = (dot_product/((mod_denom1)*(mod_denom2)));
    float cos = acos(cosnum)*180/PI;
    cout<< cos;
}
Support Ukraine
  • 42,271
  • 4
  • 38
  • 63
Harshit Joshi
  • 36
  • 4
  • don't define `PI` yourself! It's already in math.h, use `M_PI` – Jason S May 05 '16 at 18:44
  • it would also be better to use intermediate values that are equal to `x1-x2`, `x2-x3`, etc. -- the code you have is very prone to copy-paste errors. – Jason S May 05 '16 at 18:46