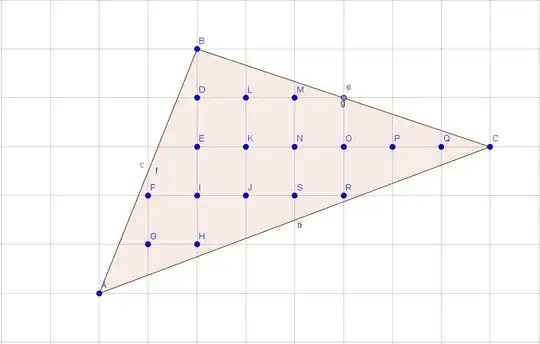
The problem input is specified by three points A, B, C, each with two coordinates x, y.
The solution should be an array of all points inside the the triangle with natural coordinates.
The input is:
A, B, C
The output is: all named point on the figure
Please note that I'm trying to calculate all the points not count them so this question differs from mine quite a bit.
What I'm having trouble with:
Mainly the problem is that, specifying all three segments would require to calculate the coefficients a, b for all segments which could extend my code quite a bit because I would have to cover all the cases of horizontal and vertical lines.
Then the best method I could come up with would be:
- Iterating through natural
x'esfrom minxof pointsA, B, Cto the max. - Iterating through natural
y'sfrom minyof pointsA, B, Cto the max. - For each point checking whether is satisfies equation system with 9 inequalities, which I could solve manually of use
numpy. The high number of inequalities is the second hardest problem.
Generally any way I can think of doing this would require me to write a lot of code with a lot of possible bugs. Also the more instructions I write, the lower the performance gets because of many non-trivial computational methods used.
Any help with a simpler solution would be much appreciated.