Detecting Diagonals in a matrix

Question

I have outputs from a process that produce a data trend as seen below:

The data output seems to have a trend with the diagonals, however I am unsure on how I can track this. Ultimately, I know the first 15 numbers in each 16 number sample, and want to predict the 16th. It seems like you should be able to do this with some type of approximation that involves matrix math or possible phase shift in a Fourier series. Is there a method that could achieve this? If there is a solution that can be used via Python that would be preferred.

I don't know if `NumPy` has a neat function for this but you could always loop over the rows and then loop over the columns and check if the `i`th element in the `j`th row is equal to the element in the `i+1`th row and `j-1`th column. Obviously make sure you put in safeguards for the index range. — turnip, Jun 05 '16 at 19:34
Also, when you say you wish to *track/detect* this trend, what do you mean? What do you want to do with it? — turnip, Jun 05 '16 at 19:40
@PPG I tried a method similar to what you described. The issue is that moving from A1 to A2 is moving forward in time so that is not necessarily known at the when trying to predict P1. This is historical data shown. I tried creating a database to search through but that had to be so large that it was moving closer and closer to 50% probability of a 0 or a 1. I want to take the first 15 numbers and determine if the 16th will be a 0 or a 1. — paperstsoap, Jun 05 '16 at 19:43
If it's as regular as you show, column 16 should just be equal to column 15, rolled by negative one on the y axis... no? — Benjamin, Jun 10 '16 at 20:11
@Benjamin Can you elaborate some. I think I understand what you are saying but not quite. — paperstsoap, Jun 10 '16 at 20:48
Use Omran Matrix, it is specially developed 2011 for exactly this case. Just multiply your image with the matrix, and you will get ones in the first row, if a diagonal exists. I would appreciate, if somebody implements it in NumPy. See my answer for detail, my paper, and PhD in which it was developed. — Sherif O., Jan 08 '22 at 18:52

Sherif O. · Answer 1 · 2022-01-09T10:00:51.307

you can use my diagonal detection matrix, it was developed for a similar issue, some times, it is referred to by Omran Matrix. All you need, is to multiply the image (your matrix) with my matrix, and summate the first row of the output, which will give you the number of diagonals in the image. The matrix is also very flexible and can be a vertical rectangular matrix, I used some tricks in the physical meaning to inverse it. I developed it in 2010 in Zurich, while doing my PhD to detect diagonal lines or overtones in sweeps in visual sound images. the matrix is published in Detecting diagonal activity to quantify harmonic structure preservation with cochlear implant mapping or formal link. The PhD thesis is called, mechanism of music perception using cochlear implants, University of Zurich, 2011 by Sherif Omran. If you write a paper, please cite me and good luck

here are similar images with overtones, I used my matrix to detect these diagonal activities, which look very near to yours.

score 0 · Answer 2 · edited May 23 '17 at 11:52

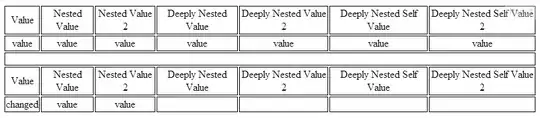
Here is an example of how to check whether opposite diagonals contain only 1s, like in your case:

In [52]: from scipy.sparse import eye

let's create a matrix with a opposite diagonal

In [53]: a = np.fliplr(eye(5, 8, k=1).toarray())

In [54]: a
Out[54]:
array([[ 0.,  0.,  0.,  0.,  0.,  0.,  1.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  1.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.,  0.,  0.,  0.]])

Flip array in the left/right direction

In [55]: f = np.fliplr(a)

In [56]: f
Out[56]:
array([[ 0.,  1.,  0.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  1.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  1.,  0.,  0.]])

the same can be done:

In [71]: a[::-1,:]
Out[71]:
array([[ 0.,  0.,  1.,  0.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  1.,  0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  1.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  1.,  0.,  0.],
       [ 0.,  0.,  0.,  0.,  0.,  0.,  1.,  0.]])

get given diagonal

In [57]: np.diag(f, k=1)
Out[57]: array([ 1.,  1.,  1.,  1.,  1.])

In [58]: np.diag(f, k=-1)
Out[58]: array([ 0.,  0.,  0.,  0.])

In [111]: a[::-1].diagonal(2)
Out[111]: array([ 1.,  1.,  1.,  1.,  1.])

check whether the whole diagonal contains 1s

In [61]: np.all(np.diag(f, k=1) == 1)
Out[61]: True

or

In [64]: (np.diag(f, k=1) == 1).all()
Out[64]: True

In [65]: (np.diag(f, k=0) == 1).all()
Out[65]: False

This answer will help you to find all diagonals

PS i'm a newbie in numpy, so i'm pretty sure there must be faster and more elegant solutions

I am going to have to read through this and the linked post with some detail to understand it. I will try to get back with you as soon as I can. — paperstsoap, Jun 05 '16 at 20:39
This looks like it would work for identifying a diagonal in a matrix, but for my problem I don't know enough information to use it accurately. — paperstsoap, Jun 06 '16 at 11:37
`rot90` is also a useful function to keep in mind in this context. — percusse, Jun 13 '16 at 12:30

Detecting Diagonals in a matrix

2 Answers2