Is an algorithm with a worst-case time complexity of O(n) always faster than an algorithm with a worst-case time complexity of O(n^2)?

Question

This question has appeared in my algorithms class. Here's my thought:

I think the answer is no, an algorithm with worst-case time complexity of O(n) is not always faster than an algorithm with worst-case time complexity of O(n^2).

For example, suppose we have total-time functions S(n) = 99999999n and T(n) = n^2. Then clearly S(n) = O(n) and T(n) = O(n^2), but T(n) is faster than S(n) for all n < 99999999.

Is this reasoning valid? I'm slightly skeptical that, while this is a counterexample, it might be a counterexample to the wrong idea.

Thanks so much!

Answer 1

Big-O notation says nothing about the speed of an algorithm for any given input; it describes how the time increases with the number of elements. If your algorithm executes in constant time, but that time is 100 billion years, then it's certainly slower than many linear, quadratic and even exponential algorithms for large ranges of inputs.

But that's probably not really what the question is asking. The question is asking whether an algorithm A1 with worst-case complexity O(N) is always faster than an algorithm A2 with worst-case complexity O(N^2); and by faster it probably refers to the complexity itself. In which case you only need a counter-example, e.g.:

• A1 has normal complexity O(log n) but worst-case complexity O(n^2).
• A2 has normal complexity O(n) and worst-case complexity O(n).

In this example, A1 is normally faster (i.e. scales better) than A2 even though it has a greater worst-case complexity.

Answer 2

You're talking about worst-case complexity here, and for some algorithms the worst case never happen in a practical application.

Saying that an algorithm runs faster than another means it run faster for all input data for all sizes of input. So the answer to your question is obviously no because the worst-case time complexity is not an accurate measure of the running time, it measures the order of growth of the number of operations in a worst case.

In practice, the running time depends of the implementation, and is not only about this number of operations. For example, one has to care about memory allocated, cache-efficiency, space/temporal locality. And obviously, one of the most important thing is the input data.

If you want examples of when the an algorithm runs faster than another while having a higher worst-case complexity, look at all the sorting algorithms and their running time depending of the input.

Answer 3

Since the question says Always it means it is enough to find only one counter example to prove that the answer is No.

Example for O(n^2) and O(n logn) but the same is true for O(n^2) and O(n)

One simple example can be a bubble sort where you keep comparing pairs until the array is sorted. Bubble sort is O(n^2). If you use bubble sort on a sorted array, it will be faster than using other algorithms of time complexity O(nlogn).

Answer 4

You are correct in every sense, that you provide a counter example to the statement. If it is for exam, then period, it should grant you full mark.

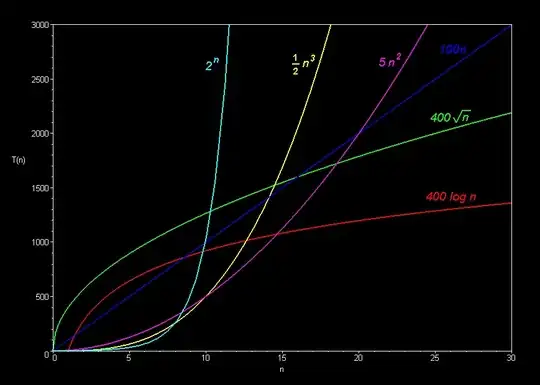
Yet for a better understanding about big-O notation and complexity stuff, I will share my own reasoning below. I also suggest you to always think the following graph when you are confused, especially the O(n) and O(n^2) line:

---

Big-O notation

My own reasoning when I first learnt computational complexity is that,

Big-O notation is saying for sufficient large size input, "sufficient" depends on the exact formula (Using the graph, n = 20 when compared O(n) & O(n^2) line), a higher order one will always be slower than lower order one

That means, for small input, there is no guarantee a higher order complexity algorithm will run slower than lower order one.

But Big-O notation tells you an information: When the input size keeping increasing, keep increasing....until a "sufficient" size, after that point, a higher order complexity algorithm will be always slower. And such a "sufficient" size is guaranteed to exist*.

---

Worst-time complexity

While Big-O notation provides a upper bound of the running time of an algorithm, depends on the structure of the input and the implementation of the algorithm, it may generally have a best complexity, average complexity and worst complexity.

The famous example is sorting algorithm: QuickSort vs MergeSort!

QuickSort, with a worst case of O(n^2)

MergeSort, with a worst case of O(n lg n)

However, Quick Sort is basically always faster than Merge Sort!

So, if your question is about Worst Case Complexity, quick sort & merge sort maybe the best counter example I can think of (Because both of them are common and famous)

---

Therefore, combine two parts, no matter from the point of view of input size, input structure, algorithm implementation, the answer to your question is NO.