As per my comment above
import numpy as np
A = np.random.random((20, 2))
A[:,0] = np.arange(20)
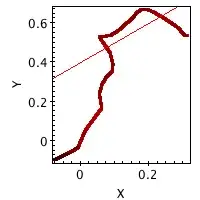
A[:,1] = A[:,1] * (7.5 + A[:,0]) # some kind of wiggly line
p0 = [-1.0,-6.5] # point 0
p1 = [22.0, 20.0] # point 1
b = (p1[1] - p0[1]) / (p1[0] - p0[0]) # gradient
a = p0[1] - b * p0[0] # intercept
B = (a + A[:,0] * b) - A[:,1] # distance of y value from line
ix = np.where(B[1:] * B[:-1] < 0)[0] # index of points where the next point is on the other side of the line
d_ratio = B[ix] / (B[ix] - B[ix + 1]) # similar triangles work out crossing points
cross_points = np.zeros((len(ix), 2)) # empty array for crossing points
cross_points[:,0] = A[ix,0] + d_ratio * (A[ix+1,0] - A[ix,0]) # x crossings
cross_points[:,1] = A[ix,1] + d_ratio * (A[ix+1,1] - A[ix,1]) # y crossings
print(ix, B, A, cross_points)
 – Julia Roquette
Jun 21 '16 at 18:49
– Julia Roquette
Jun 21 '16 at 18:49