Produce nice linear regression plot (fitted line, confidence / prediction bands, etc)

Question

I have this sample 10-year regression in the future.

date<-as.Date(c("2015-12-31", "2014-12-31", "2013-12-31", "2012-12-31"))
value<-c(16348, 14136, 12733, 10737)
#fit linear regression
model<-lm(value~date)
#build predict dataframe
dfuture<-data.frame(date=seq(as.Date("2016-12-31"), by="1 year", length.out = 10))
#predict the futurne
predict(model, dfuture, interval = "prediction")

How can I add confidence bands to this?

Possible duplicate of [How to calculate the 95% confidence interval for the slope in a linear regression model in R](http://stackoverflow.com/questions/15180008/how-to-calculate-the-95-confidence-interval-for-the-slope-in-a-linear-regressio) — majom, Jul 05 '16 at 16:17
It is no duplicate of the above mentioned. The OP was asking for a confidence band and not a confidence interval. — Alex, Jul 05 '16 at 16:21
@Zheyuan Li I also would not think that it is a duplicate of that. First the terminology is used oddly. If somebody is looking for it and uses the right terms he probably will not find it. Second, we have here the special case of a linear regression which is not mentioned in the other answer. Surprisingly (also for me), you won't get a good result if you look for `[r] confidence band linear regressions`. So I think the question is fine. But I am also sure that there are plenty solutions for this on SO. But how can they help if you cannot find them? — Alex, Jul 06 '16 at 07:04

score 5 · Accepted Answer · edited May 23 '17 at 12:00

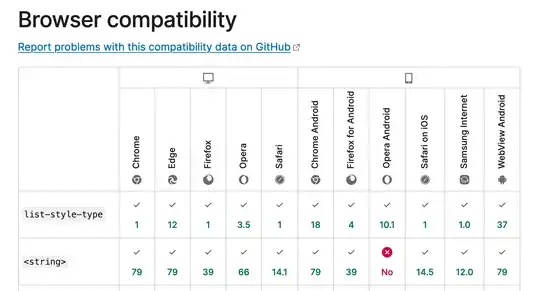
The following code will generate good-looking regression plot for you. My comments along the code should explain everything clear. The code will use value, model as in your question.

## all date you are interested in, 4 years with observations, 10 years for prediction
all_date <- seq(as.Date("2012-12-31"), by="1 year", length.out = 14)

## compute confidence bands (for all data)
pred.c <- predict(model, data.frame(date=all_date), interval="confidence")

## compute prediction bands (for new data only)
pred.p <- predict(model, data.frame(date=all_date[5:14]), interval="prediction")

## set up regression plot (plot nothing here; only set up range, axis)
ylim <- range(range(pred.c[,-1]), range(pred.p[,-1]))
plot(1:nrow(pred.c), numeric(nrow(pred.c)), col = "white", ylim = ylim,
     xaxt = "n", xlab = "Date", ylab = "prediction",
     main = "Regression Plot")
axis(1, at = 1:nrow(pred.c), labels = all_date)

## shade 95%-level confidence region
polygon(c(1:nrow(pred.c),nrow(pred.c):1), c(pred.c[, 2], rev(pred.c[, 3])),
        col = "grey", border = NA)

## plot fitted values / lines
lines(1:nrow(pred.c), pred.c[, 1], lwd = 2, col = 4)

## add 95%-level confidence bands
lines(1:nrow(pred.c), pred.c[, 2], col = 2, lty = 2, lwd = 2)
lines(1:nrow(pred.c), pred.c[, 3], col = 2, lty = 2, lwd = 2)

## add 95%-level prediction bands
lines(4 + 1:nrow(pred.p), pred.p[, 2], col = 3, lty = 3, lwd = 2)
lines(4 + 1:nrow(pred.p), pred.p[, 3], col = 3, lty = 3, lwd = 2)

## add original observations on the plot
points(1:4, rev(value), pch = 20)

## finally, we add legend
legend(x = "topleft", legend = c("Obs", "Fitted", "95%-CI", "95%-PI"),
       pch = c(20, NA, NA, NA), lty = c(NA, 1, 2, 3), col = c(1, 4, 2, 3),
       text.col = c(1, 4, 2, 3), bty = "n")

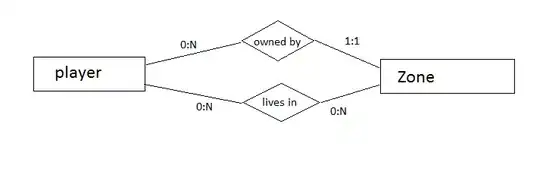
The JPEG is generated by code:

jpeg("regression.jpeg", height = 500, width = 600, quality = 100)
## the above code
dev.off()
## check your working directory for this JPEG
## use code getwd() to see this director if you don't know

As you can see from the plot,

Confidence band grows wider as you try to make prediction further away from you observed data;
Prediction interval is wider than confidence interval.

If you want to know more about how predict.lm() computes confidence / prediction intervals internally, read How does predict.lm() compute confidence interval and prediction interval?, and my answer there.

Thanks to Alex's demonstration of simple use of visreg package; but I still prefer to using R base.

I think you use the terms in a different way than me. For prediction I would call it prediction band as wikipedia does https://en.wikipedia.org/wiki/Confidence_and_prediction_bands#Prediction_bands. The term confidence interval I would use for the interval of the regression parameters as described here: https://en.wikipedia.org/wiki/Confidence_interval. — Alex, Jul 06 '16 at 06:45
@ZheyuanLi can these two plots be displayed as one, as a continuum? I mean, starting out as in your bottom plot but then continuing as in your top plot? — Oposum, Jul 07 '16 at 01:04

score 2 · Answer 2 · answered Jul 05 '16 at 16:15

2

You can simply use visreg::visreg

library(visreg)
visreg(model)

If you are interested in the values:

> head(visreg(model)$fit)
        date   value visregFit visregLwr visregUpr
1 2012-12-31 13434.5  10753.10  9909.073  11597.13
2 2013-01-10 13434.5  10807.81  9974.593  11641.02
3 2013-01-21 13434.5  10862.52 10040.033  11685.00
4 2013-02-01 13434.5  10917.22 10105.389  11729.06
5 2013-02-12 13434.5  10971.93 10170.658  11773.21
6 2013-02-23 13434.5  11026.64 10235.837  11817.44

answered Jul 05 '16 at 16:15

Alex

4,925
2
32
48

sorry I meant, why does Y axis have different values compared to the previous plot? – Oposum Jul 06 '16 at 01:09
@ Oposum I think it is because the other plot used future data. But if you are doing this you should not use a confident band but a prediction band. The confidence band is related to the data you used for the estimation of the regression line. Whereas the prediction band should be used for new data. – Alex Jul 06 '16 at 06:50
I see now, I meant prediction bands. Can confidence bands and prediction bands be displayed in a continuum? – Oposum Jul 07 '16 at 01:02

Produce nice linear regression plot (fitted line, confidence / prediction bands, etc)

2 Answers2