I've read the answers to this question and they are quite helpful, but I need help.
I have an example data set in R as follows:
x <- c(32,64,96,118,126,144,152.5,158)
y <- c(99.5,104.8,108.5,100,86,64,35.3,15)
I want to fit a model to these data so that y = f(x). I want it to be a 3rd order polynomial model.
How can I do that in R?
Additionally, can R help me to find the best fitting model?
To get a third order polynomial in x (x^3), you can do
lm(y ~ x + I(x^2) + I(x^3))
or
lm(y ~ poly(x, 3, raw=TRUE))
You could fit a 10th order polynomial and get a near-perfect fit, but should you?
EDIT: poly(x, 3) is probably a better choice (see @hadley below).
Which model is the "best fitting model" depends on what you mean by "best". R has tools to help, but you need to provide the definition for "best" to choose between them. Consider the following example data and code:
x <- 1:10
y <- x + c(-0.5,0.5)
plot(x,y, xlim=c(0,11), ylim=c(-1,12))
fit1 <- lm( y~offset(x) -1 )
fit2 <- lm( y~x )
fit3 <- lm( y~poly(x,3) )
fit4 <- lm( y~poly(x,9) )
library(splines)
fit5 <- lm( y~ns(x, 3) )
fit6 <- lm( y~ns(x, 9) )
fit7 <- lm( y ~ x + cos(x*pi) )
xx <- seq(0,11, length.out=250)
lines(xx, predict(fit1, data.frame(x=xx)), col='blue')
lines(xx, predict(fit2, data.frame(x=xx)), col='green')
lines(xx, predict(fit3, data.frame(x=xx)), col='red')
lines(xx, predict(fit4, data.frame(x=xx)), col='purple')
lines(xx, predict(fit5, data.frame(x=xx)), col='orange')
lines(xx, predict(fit6, data.frame(x=xx)), col='grey')
lines(xx, predict(fit7, data.frame(x=xx)), col='black')
Which of those models is the best? arguments could be made for any of them (but I for one would not want to use the purple one for interpolation).
Regarding the question 'can R help me find the best fitting model', there is probably a function to do this, assuming you can state the set of models to test, but this would be a good first approach for the set of n-1 degree polynomials:
polyfit <- function(i) x <- AIC(lm(y~poly(x,i)))
as.integer(optimize(polyfit,interval = c(1,length(x)-1))$minimum)
Notes
The validity of this approach will depend on your objectives, the assumptions of optimize() and AIC() and if AIC is the criterion that you want to use,
polyfit() may not have a single minimum. check this with something like:
for (i in 2:length(x)-1) print(polyfit(i))
I used the as.integer() function because it is not clear to me how I would interpret a non-integer polynomial.
for testing an arbitrary set of mathematical equations, consider the 'Eureqa' program reviewed by Andrew Gelman here
Update
Also see the stepAIC function (in the MASS package) to automate model selection.
The easiest way to find the best fit in R is to code the model as:
lm.1 <- lm(y ~ x + I(x^2) + I(x^3) + I(x^4) + ...)
After using step down AIC regression
lm.s <- step(lm.1)
For example, if we want to fit a polynomial of degree 2, we can directly do it by solving a system of linear equations in the following way:
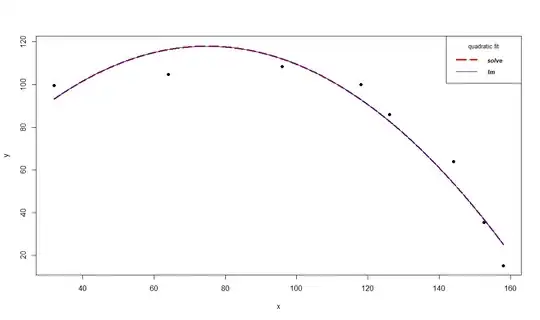
The following example shows how to fit a parabola y = ax^2 + bx + c using the above equations and compares it with lm() polynomial regression solution. Hope this will help in someone's understanding,
x <- c(32,64,96,118,126,144,152.5,158)
y <- c(99.5,104.8,108.5,100,86,64,35.3,15)
x4 <- sum(x^4)
x3 <- sum(x^3)
x2 <- sum(x^2)
x1 <- sum(x)
yx1 <- sum(y*x)
yx2 <- sum(y*x^2)
y1 <- sum(y)
A <- matrix(c(x4, x3, x2,
x3, x2, x1,
x2, x1, length(x)), nrow=3, byrow=TRUE)
B <- c(yx2,
yx1,
y1)
coef <- solve(A, B) # solve the linear system of equations, assuming A is not singular
coef1 <- lm(y ~ x + I(x^2))$coef # solution with lm
coef
# [1] -0.01345808 2.01570523 42.51491582
rev(coef1)
# I(x^2) x (Intercept)
# -0.01345808 2.01570523 42.51491582
plot(x, y, xlim=c(min(x), max(x)), ylim=c(min(y), max(y)+10), pch=19)
xx <- seq(min(x), max(x), 0.01)
lines(xx, coef[1]*xx^2+coef[2]*xx+coef[3], col='red', lwd=3, lty=5)
lines(xx, coef1[3]*xx^2+ coef1[2]*xx+ coef1[1], col='blue')
legend('topright', legend=c("solve", "lm"),
col=c("red", "blue"), lty=c(5,1), lwd=c(3,1), cex=0.8,
title="quadratic fit", text.font=4)
