How to generate random positions with distance between them?

Question

Assume that I have a vector with 6 distance elements as

D = [10.5 44.8 30.01 37.2 23.4 49.1].

I'm trying to create random pair positions of a given distances, inside a 200 meters circle. Note that the distance D created by using (b - a).*rand(6,1) + a, with a = 10 and b = 50 in Matlab. I do not know how to generate the random pairs with given the distances.

Could anybody help me in generating this kind of scenario?

so do you want to get `a` and `b` given that you know the relation `D = (b - a).*rand(6,1) + a`? — Autonomous, Jul 16 '16 at 21:47

AlessioX · Answer 1 · 2016-07-17T13:23:50.113

You can tackle the problem using a two-steps approach. You can

randomly generate the first point and then you can consider the circle whose center is that point and whose radius is the distance in D
once you did draw the circle, every point lying on that circle will have distance D from the first point previously created and by random selection of one of these candidates you'll have the second point

Let's see with an example: let's say you main circle has radius 200 and its center is (0,0) so we start by declaring some main variables.

MAINCENTER_x=0;
MAINCENTER_y=0;
MAINRADIUS=200;

Let's now consider the first distance, D(1)=10.5 and we now generate the first random point which (along with its paired point - I reckon you don't want one point inside and the other outside of the main circle) must lie inside the main circle

r=D(1); % let's concentrate on the first distance
while true
    x=((MAINRADIUS-2*r) - (-MAINRADIUS+2*r))*rand(1,1) + (-MAINRADIUS+2*r);
    y=((MAINRADIUS-2*r) - (-MAINRADIUS+2*r))*rand(1,1) + (-MAINRADIUS+2*r);
    if x^2+y^2<=(MAINRADIUS-2*r)^2
        break;
    end
end

and at the end of this loop x and y will be our first point coordinates.

Now we shall generate all its neighbours, thus several candidates to be the second point in the pair. As said before, these candidates will be the points that lie on the circle whose center is (x,y) and whose radius is D(1)=10.5. We can create these candidates as follows:

% declare angular spacing
ang=0:0.01:2*pi; 
% build neighbour points
xp=r*cos(ang)+x;
yp=r*sin(ang)+y;

Now xp and yp are two vectors that contain, respectively, the x-coordinates and y-coordinates of our candidates, thus we shall now randomly select one of these

% second point
idx=randsample(1:length(xp),1);
secondPoint_x=xp(idx);
secondPoint_y=yp(idx);

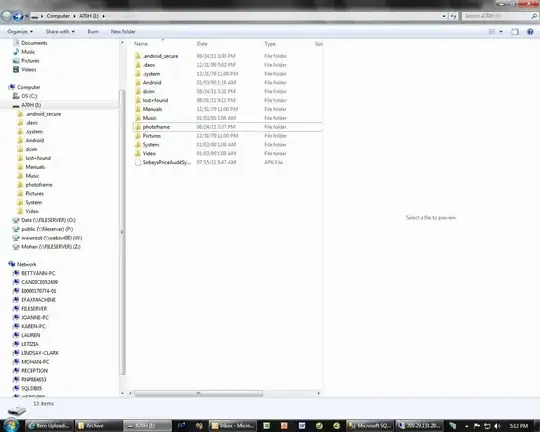
Finally, the pair (x,y) is the first point and the pair (secondPoint_x, secondPoint_y) is our second point. The following plot helps summarizing these steps: The red circle is the main area (center in (0,0) and radius 200), the red asterisk is the first point (x,y) the blue little circle has center (x,y) and radius 10.5 and finally the black asterisk is the second point of the pair (secondPoint_x, secondPoint_y), randomly extracted amongst the candidates lying on the blue little circle.

You must certainly can repeat the same process for all elements in D or rely on the following code, which does the very same thing without iterating through all the elements in D.

MAINCENTER_x=0;
MAINCENTER_y=0;
MAINRADIUS=200;

D = [10.5 44.8 30.01 37.2 23.4 49.1];

% generate random point coordinates
while true
    x=((MAINRADIUS-2*D) - (-MAINRADIUS+2*D)).*rand(1,6) + (-MAINRADIUS+2*D);
    y=((MAINRADIUS-2*D) - (-MAINRADIUS+2*D)).*rand(1,6) + (-MAINRADIUS+2*D);
    if all(x.^2+y.^2<=(MAINRADIUS-2*D).^2)
        break;
    end
end

% declare angular spacing
ang=0:0.01:2*pi; 
% build neighbour points
xp=bsxfun(@plus, (D'*cos(ang)),x');
yp=bsxfun(@plus, (D'*sin(ang)),y');

% second points
idx=randsample(1:size(xp,2),length(D));
secondPoint_x=diag(xp(1:length(D),idx));
secondPoint_y=diag(yp(1:length(D),idx));
%plot
figure(1);
plot(MAINRADIUS*cos(ang)+MAINCENTER_x,MAINRADIUS*sin(ang)+MAINCENTER_y,'r'); %main circle
hold on; plot(xp',yp');                          % neighbours circles
hold on; plot(x,y,'r*');                         % first points (red asterisks)
hold on; plot(secondPoint_x,secondPoint_y,'k*'); %second points (black asterisks)
axis equal;

Now x and y (and secondPoint_x and secondPoint_y by extension) will be vector of length 6 (because 6 are the distances) in which the i-th element is the i-th x (or y) component for the first (or second) point.

Why don't you generate your random points in polar coordinates? Then you can remove the `while` loop and generating lots of candidate neighbors. — saastn, Jul 17 '16 at 11:21
Thanks a lot @Alessiox. Alessiox! Could you give me the code how to plot the circle with the different color in you figure? — user3727281, Jul 17 '16 at 13:18
@Alessiox Hi, could you explaint me what does it mean about randsample and diag function to generate the second points? Thanks a lot — user3727281, Jul 17 '16 at 22:24
@user3727281 you can as well read the Matlab docs but, in short, `randsample(A,B)` selects `B` points at random from population `A` whereas `diag` selects elements from the diagonal of a matrix. More into details, with `randsample` we select 6 IDs amongst the number of neighbours because we have 6 distances, thus one-per-distance. The `diag` helps us returning the 6 values after mapping with integers 1-6 — AlessioX, Jul 18 '16 at 06:48
@user3727281 Before the `diag` command we have 6 indices (`idx`) and our goal is to take the column corresponding to the first index from the first row of `xp`, the column corresponding to the second index from the second row of `xp` and so on (and same story goes for `yp`). As an alternative for `diag`, you can use `sub2ind()` as follows `secondPoint_x=xp(sub2ind(size(xp), 1:size(xp,1), idx));` (and same story goes for `yp`). — AlessioX, Jul 18 '16 at 07:44

score 0 · Accepted Answer · edited May 23 '17 at 12:32

0

This is an improvement to Alessiox's answer. It follows same logic, first generate a set of points ([X1 Y1]) that have at least distance D from the main circle border, then generate the second set of points ([X2 Y2]) that have exact distance D from the first set.

cx = 50; cy = -50; cr = 200;
D = [10.5 44.8 30.01 37.2 23.4 49.1]';
n = numel(D);

R1 = rand(n, 1) .* (cr - D);
T1 = rand(n, 1) * 2 * pi;
X1 = cx+R1.*cos(T1);
Y1 = cy+R1.*sin(T1);

T2 = rand(n, 1) * 2 * pi;
X2 = X1+D.*cos(T2);
Y2 = Y1+D.*sin(T2);

edited May 23 '17 at 12:32

Community

1
1

answered Jul 17 '16 at 11:46

saastn

5,717
8
47
78

Thanks you very much for your helping @ saastn Could you post the code how to draw the circle? – user3727281 Jul 17 '16 at 13:19
@user3727281 sure, I use **Method 12** from [here](http://stackoverflow.com/a/37990100/2093077) – saastn Jul 17 '16 at 13:25
Thanks a lot @ saastn – user3727281 Jul 17 '16 at 13:29
How do you think in another case that the second point have a position outside the circle? Because I want all of points inside the circle? How can you fix it? Thanks – user3727281 Jul 17 '16 at 13:58
@ saastn I have a mistake in the code, and i fixed it. Thanks a lot. – user3727281 Jul 17 '16 at 14:11
@ saastn. With the same idea, instead the circle. I want to put the points inside of hexagol. The mistate is any second point ouside of hexagol. How do you know how can I fix it? Thanks a lot. – user3727281 Jul 17 '16 at 14:30
@user3727281 Well that changes everything, you should ask another question. – saastn Jul 17 '16 at 14:58

How to generate random positions with distance between them?

2 Answers2

Linked