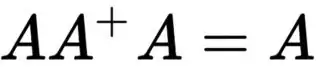octave:1> A = [1 2 3; 4 5 6; 7 8 9]
octave:2> B = pinv (A)
octave:3> I = eye (size (A))
ans =
Diagonal Matrix
1 0 0
0 1 0
0 0 1
octave:4> I2 = A * B
ans =
0.83333 0.33333 -0.16667
0.33333 0.33333 0.33333
-0.16667 0.33333 0.83333
octave:5> A2 = A * I2
ans =
1.00000 2.00000 3.00000
4.00000 5.00000 6.00000
7.00000 8.00000 9.00000
Why could the final Step 5 result in the perfect accuracy although the previous Step 4 in the unforgiving accuracy?
@EDIT
octave:6> format long
octave:7> I2
I2 =
0.833333333333332 0.333333333333332 -0.166666666666666
0.333333333333332 0.333333333333333 0.333333333333334
-0.166666666666668 0.333333333333333 0.833333333333334
octave:8> A2
A2 =
0.999999999999993 1.999999999999997 3.000000000000005
3.999999999999982 4.999999999999992 6.000000000000014
6.999999999999972 7.999999999999987 9.000000000000021