It's problematic, but the standard unfortunately does not specify in detail what algorithm to use when constructing (many) of the randomly distributed numbers, and there are several valid alternatives, with different benefits.
26.6.8.5 Normal distributions [rand.dist.norm]
26.6.8.5.1 Class template normal_distribution [rand.dist.norm.normal]
A normal_distribution random number distribution produces random
numbers x distributed according to the probability density function
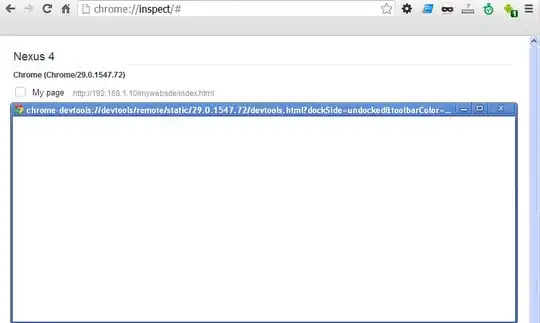
parameters μ and are also known as this distribution’s mean and
standard deviation .
The most common algorithm for generating normally distributed numbers is Box-Muller, but even with that algorithm there are options and variations.
The freedom is even explicitly mentioned in the standard:
26.6.8 Random number distribution class templates [rand.dist]
. . .
3 The
algorithms for producing each of the specified distributions are
implementation-defined.
A goto option for this is boost random
By the way, as @Hurkyl points out: It seems that the two implementations are actually the same: For example box-muller generates pairs of values, of which one is returned and one is cached. The two implementations differ only in which of the values is returned.
Further, the random number engines are completely specified and will give the same sequence between implementations, but care does need to be taken since the different distributions can also consume different amounts of random data in order to produce their results, which will put the engines out of sync.