How to use the reduced data - the output of principal component analysis

Question

I am finding it hard to link the theory with the implementation. I would appreciate help in knowing where my understanding is wrong.

Notations - matrix in bold capital and vectors in bold font small letter

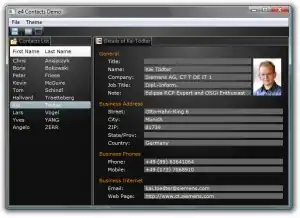is a dataset on observations, each of variables. So, given these observed -dimensional data vectors, the 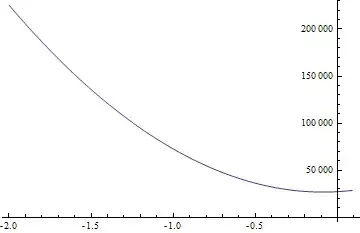-dimensional principal axes are , for in where is the target dimension.

The principal components of the observed data matrix would be where matrix , matrix , and matrix .

Columns of form an orthogonal basis for the features and the output 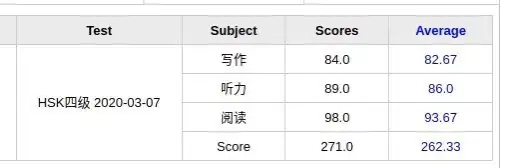is the principal component projection that minimizes the squared reconstruction error:

and the optimal reconstruction of is given by .

The data model is

X(i,j) = A(i,:)*S(:,j) + noise

where PCA should be done on X to get the output S. S must be equal to Y.

Problem 1: The reduced data Y is not equal to S that is used in the model. Where is my understanding wrong?

Problem 2: How to reconstruct such that the error is minimum?

Please help. Thank you.

   clear all
clc
n1 = 5; %d dimension
n2 = 500; % number of examples

ncomp = 2; % target reduced dimension
%Generating data according to the model
% X(i,j) = A(i,:)*S(:,j) + noise
Ar = orth(randn(n1,ncomp))*diag(ncomp:-1:1);
T = 1:n2;
%generating synthetic data from a dynamical model
S = [ exp(-T/150).*cos( 2*pi*T/50 )
       exp(-T/150).*sin( 2*pi*T/50 ) ];
% Normalizing to zero mean and unit variance
S = ( S - repmat( mean(S,2), 1, n2 ) );
S = S ./ repmat( sqrt( mean( Sr.^2, 2 ) ), 1, n2 );
Xr = Ar * S;
Xrnoise = Xr + 0.2 * randn(n1,n2);

h1 = tsplot(S);


    X = Xrnoise;

XX = X';
[pc, ~] = eigs(cov(XX), ncomp);
Y = XX*pc;

UPDATE [10 Aug]

Based on the Answer, here is the full code that

 clear all
clc
n1 = 5; %d dimension
n2 = 500; % number of examples

ncomp = 2; % target reduced dimension
%Generating data according to the model
% X(i,j) = A(i,:)*S(:,j) + noise
Ar = orth(randn(n1,ncomp))*diag(ncomp:-1:1);
T = 1:n2;
%generating synthetic data from a dynamical model
S = [ exp(-T/150).*cos( 2*pi*T/50 )
       exp(-T/150).*sin( 2*pi*T/50 ) ];
% Normalizing to zero mean and unit variance
S = ( S - repmat( mean(S,2), 1, n2 ) );
S = S ./ repmat( sqrt( mean( S.^2, 2 ) ), 1, n2 );
Xr = Ar * S;
Xrnoise = Xr + 0.2 * randn(n1,n2);

    X = Xrnoise;

XX = X';
[pc, ~] = eigs(cov(XX), ncomp);
Y = XX*pc; %Y are the principal components of X' 
%what you call pc is misleading, these are not the principal components
%These Y columns are orthogonal, and should span the same space 
%as S approximatively indeed (not exactly, since you introduced noise).

%If you want to reconstruct 
%the original data can be retrieved by projecting 
%the principal components back on the original space like this:
Xrnoise_reconstructed = Y*pc';

%Then, you still need to project it through 
%to the S space, if you want to reconstruct S
S_reconstruct = Ar'*Xrnoise_reconstructed';


plot(1:length(S_reconstruct),S_reconstruct,'r')
hold on
 plot(1:length(S),S)

The plot is 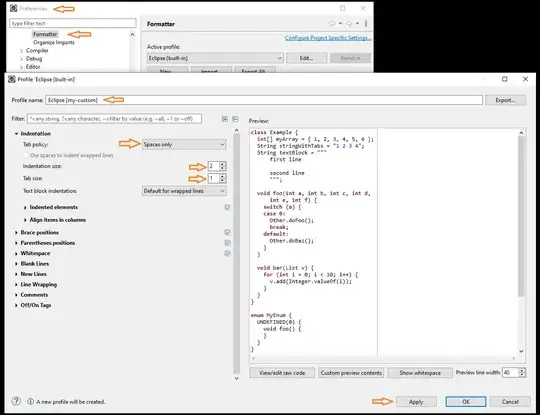which is very different from the one that is shown in the Answer. Only one component of S exactly matches with that of S_reconstructed. Shouldn't the entire original 2 dimensional space of the source input S be reconstructed? Even if I cut off the noise, then also onely one component of S is exactly reconstructed.

Answer 1

I see nobody answered your question, so here goes:

What you computed in Y are the principal components of X' (what you call pc is misleading, these are not the principal components). These Y columns are orthogonal, and should span the same space as S approximatively indeed (not exactly, since you introduced noise).

If you want to reconstruct Xrnoise, you must look at the theory (e.g. here) and apply it correctly: the original data can be retrieved by projecting the principal components back on the original space like this:

Xrnoise_reconstructed = Y*pc'

Then, you still need to transform it through pinv(Ar)*Xrnoise_reconstructed, if you want to reconstruct S.

Matches nicely for me:

answer to UPDATE [10 Aug]: (EDITED 12 Aug)

Your Ar matrix does not define an orthonormal basis, and as such, the transpose Ar' is not the reverse transformation. The earlier answer I provided was thus wrong. The answer has been corrected above.

Answer 2

Your understanding is quite right. One of the reasons for somebody to use PCA would be to reduce the dimensionality of the data. The first principal component has the largest sample variance amongst of all the normalized linear combinations of the columns of X. The second principal component has maximum variance subject to being orthogonal to the next one, etc.

One might then do a PCA on a dataset, and decide to cut off the last principal component or several of the last principal components of the data. This is done to reduce the effect of the curse of dimensionality. The curse of dimensionality is a term used to point out the fact that any group of vectors is sparse in a relatively high dimensional space. Conversely, this means that you would need an absurd amount of data to form any model on a fairly high dimension dataset, such as an word histogram of a text document with possibly tens of thousands of dimensions.

In effect a dimensionality reduction by PCA removes components that are strongly correlated. For example let's take a look at a picture:

As you can see, most of the values are almost the same, strongly correlated. You could meld some of these correlated pixels by removing the last principal components. This would reduce the dimensionality of the image, pack it, by removing some of the information in the image.

There is no magic way to determine the best amount of principal components or the best reconstruction that I'm aware of.

Answer 3

Forgive me if i am not mathematically rigorous. If we look at the equation: X = A*S we can say that we are taking some two dimensional data and we map it to a 2 dimensional subspace in 5 dimensional space. Were A is some base for that 2 dimensional subspace.

When we solve the PCA problem for X and look at PC (principal compononet) we see that the two big eignvectors (which coresponds to the two largest eignvalues) span the same subspace that A did. (multpily A'*PC and see that for the first three small eignvectors we get 0 which means that the vectors are orthogonal to A and only for the two largest we get values that are different than 0).

So what i think that the reason why we get a different base for this two dimensional space is because X=A*S can be product of some A1 and S1 and also for some other A2 and S2 and we will still get X=A1*S1=A2*S2. What PCA gives us is a particular base that maximize the variance in each dimension.

So how to solve the problem you have? I can see that you chose as the testing data some exponential times sin and cos so i think you are dealing with a specific kind of data. I am not an expert in signal processing but look at MUSIC algorithm.

Answer 4

You could use the pca function from Statistics toolbox.

coeff = pca(X)

From documentation, each column of coeff contains coefficients for one principal component. So you can reconstruct the observed data X by multiplying with coeff, e.g. X*coeff