first n digits of an exponentiation

Question

How do i determine the first n digits of an exponentiation (a^b).

eg: for a = 12, b = 13 & n = 4, the first 4 digits are 1069.

I see http://stackoverflow.com/questions/635183/fast-exponentiation-when-only-first-k-digits-are-required but i don't get the clear picture. Cld someone elaborate briefly. — josh, Oct 06 '10 at 14:05
Wouldn't this be better on math.stackexchange? I don't see a programming question here. — Mark B, Oct 06 '10 at 14:49
@Mark B: Considering the languages it was tagged in, and the fact that `snprintf` or the C++ equivalent is likely one possible implementation that does not require writing the algorithm yourself, I think this question is completely appropriate on SO. — R.. GitHub STOP HELPING ICE, Oct 06 '10 at 15:34
@R The question didn't state that you were allowed to restrict yourself to the set of values representable by a `double` and I assumed they could be arbitrary. Developing the appropriate algorithm to generate just the first `n` digits would be more appropriate for math.stackexchange. — Mark B, Oct 06 '10 at 15:58
I've asked similarly mathematical questions here from a programming standpoint before (http://stackoverflow.com/questions/3215235/how-do-you-print-the-exact-value-of-a-floating-point-number) and never had anyone question whether it's off-topic. — R.. GitHub STOP HELPING ICE, Oct 06 '10 at 16:14

score 21 · Accepted Answer · edited Oct 08 '10 at 04:54

Calculate a^b by the following iterations:

a₁ = a¹,
a₂ = a²,
...
a_i = aⁱ,
...
a_b = a^b

You have a_i+1 = a_i×a. Calcluate each a_i not exactly. The thing is that the relative error of a^b is less than n times relative error of a.
You want to get final relative error less than 10^-n. Thus relative error on each step may be 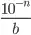forumula . Remove last digits at each step.

For example, a=2, b=16, n=1. Final relative error is 10^-n = 0.1. Relative error on each step is 0.1/16 > 0.001. Thus 3 digits is important on each step. If n = 2, you must save 4 digits. Common rule: save [n+log₁₀ b] digits at each step.

2 (1), 4 (2), 8 (3), 16 (4), 32 (5), 64 (6), 128 (7), 256 (8), 512 (9), 1024 (10) → 102,
204 (11), 408 (12), 816 (13), 1632 (14) → 163, 326 (15), 652 (16).

Answer: 6.

This algorithm has a compexity of O(b). But it is easy to change it to get O(log b)

How relative error on each step is (10^(-n))/b, means how to derive it? Can you please explain? — Saurabh, Jun 21 '13 at 15:49

score 6 · Answer 2 · answered Aug 25 '13 at 18:15

6

n=9 k=3 n^n=387420489 and answer should be 387

enter image description here

this is the same thing, what @RC as done in his code. Thank you @RC i just showed the mathematic representation your code.

answered Aug 25 '13 at 18:15

Madan Ram

880
1
11
18

score 6 · Answer 3 · answered Oct 08 '10 at 05:31

Another solution, using log10:

#include <stdio.h>
#include <stdlib.h>
#include <math.h>

int main(int argc, char **argv) {
       int a = 12;
       int b = 13;
       int n = 4;
       double x, y;

       x = b * log10(a);
       y = floor(pow(10, x - floor(x) + n - 1));
       printf("Result: %d\n", (int)y);

       return EXIT_SUCCESS;
}

Steve Townsend · Answer 4 · 2010-10-06T15:36:52.620

1

For this case - with magic numbers 12,13,4 in place:

#include <sstream>
#include <iomanip>
#include <cmath>

double a = 12;
int b = 13;
double result = std::pow(a,b);

std::stringstream strVal;
strVal.setf( ios::fixed, ios::floatfield );
strVal << result;
std::string output(strVal.str().substr(0,4));

output = "1069"

std::stringstream intStr(output);
int intVal;
intStr >> intVal;

intVal = 1069

EDIT: This should work for any combination where result does not overflow double.

edited Oct 06 '10 at 15:36

answered Oct 06 '10 at 15:00

Steve Townsend

53,498
9
91
140

Is this correct even for huge numbers as long as the result does not overflow `double`? I suspect so, but it would be worth discussing as part of a complete answer. – R.. GitHub STOP HELPING ICE Oct 06 '10 at 15:12
@R.. - good point, edited to use `long double` and added comment – Steve Townsend Oct 06 '10 at 15:20
`long double` is likely the same as `double` on Windows. Some analysis of whether the code will be subject to floating point imprecision would be better than just throwing bigger types at it to sweep the issue under the rug. – R.. GitHub STOP HELPING ICE Oct 06 '10 at 15:32
@R.. - it's as accurate as runtime library's pow function isn't it? Am I missing your point? – Steve Townsend Oct 06 '10 at 15:39
Unless your system's floating point to decimal conversion is better than any specification requires, it will fail with `n>DECIMAL_DIG`, even if `pow(a,b)` is exactly representable (which will always be the case if `a` is a power of 2). Whether there are other failure cases, I'm not sure. I think it's fine as long as `n` is significantly smaller than `DECIMAL_DIG`. – R.. GitHub STOP HELPING ICE Oct 06 '10 at 15:46
@R.. - thanks - on Windows you can optionally use SSE2 to support pow. Not sure if that affects the accuracy, or just performance. – Steve Townsend Oct 06 '10 at 15:51
Sure. BTW, "What are the first 100 digits of 2^10000?" is a perfectly reasonable question where the `pow(2,10000)` would work (for 80-bit or higher `long double`) but where the standard library might not be able to print 100 accurate decimal digits. For what it's worth, glibc will do it correctly and MSVCRT will not. – R.. GitHub STOP HELPING ICE Oct 06 '10 at 16:12

score 0 · Answer 5 · answered Oct 06 '10 at 15:02

The easiest way programatically to do this is to use a stringstream to convert the result of the exponentation to a string and then take the n most significant (i.e. left) characters.

if you want a way without strings then this will work:

#include <iostream>
#include <sstream>
#include <math.h>

using namespace std;

double nDigExp( double a, double b, int n )
{
    stringstream ss;
    ss.setf( ios::fixed, ios::floatfield );
    ss << pow(a,b);
    double ret;
    for ( int i = 0; i < n; ++i) ret = (10 * ret) + (ss.get() - '0'); // Yeuch!!
    return ret;
}

int main( )
{
    double result = nDigExp( 12, 13, 4 );

    cout << result << endl;

    return 0;
}

But it's hardly the most elegent code. I'm sure you can improve it.

first n digits of an exponentiation

5 Answers5

Linked