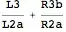The area can be directly calculated from the covariance matrix by calculating the eigenvalues first.
You need to scale the variances / eigenvalues by the factor of confidence that you want to get.
This thread is very helpful
set.seed(1234)
dat <- data.frame(x = rnorm(1:1000), y = rnorm(1:1000))
cov_dat <- cov(dat) # covariance matrix
eig_dat <- eigen(cov(dat))$values #eigenvalues of covariance matrix
vec <- sqrt(5.991* eig_dat) # half the length of major and minor axis for the 95% confidence ellipse
pi * vec[1] * vec[2]
#> [1] 18.38858
Created on 2020-02-27 by the reprex package (v0.3.0)
In this particular case, the covariances are zero, and the eigenvalues will be more or less the variance of the variables. So you can use just the variance for your calculation. - given that both are normally distributed.
set.seed(1234)
data <- data.frame(x = rnorm(1:1000), y = rnorm(1:1000))
pi * 5.991 * sd(data$x) * sd(data$y) # factor for 95% confidence = 5.991
#> [1] 18.41814
Created on 2020-02-27 by the reprex package (v0.3.0)
The calculated value is different from user eipi10's answer. This is likely due to the different calculation under the hood, with different assumptions on the underlying distribution. see this thread.