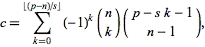So far I have managed to find the particular solution to this equation for any given mass and drag coefficient. I have not however found a way to plot the solution or even evaluate the solution for a specific point. I really want to find a way to plot the solution.
from sympy import *
m = float(raw_input('Mass:\n> '))
g = 9.8
k = float(raw_input('Drag Coefficient:\n> '))
f = Function('f')
f1 = g * m
t = Symbol('t')
v = Function('v')
equation = dsolve(f1 - k * v(t) - m * Derivative(v(t)), 0)
C1 = Symbol('C1')
C1_ic = solve(equation.rhs.subs({t:0}),C1)[0]
equation = equation.subs({C1:C1_ic})