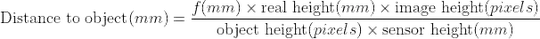I'd extend the lines of the tile till they touch the edge where the back wall meets the floor. Using this technique you can transfer a length from the wall plane to an equal length in the floor plane. So at that point, all you have to do is match lengths along a single line, namely the lengths between planks and the lengths between your transferred points. But you have to do this in a projectively consistent fashion. The most versatile tool for projective measurements is the cross ratio. An application very similar to what you have here is described in How to calculate true lengths from perspective projection on Math SE. If your vanishing point on that line where the walls meet is indeed at infinity (which appears to be approximately the case in your setup), you can get by with some simpler computations, but unless you can guarantee that this will always be the case, I'd not rely on that.
The above will help you adjust the scale in one direction only. The direction perpendicular to that is still open, though. In your exaple that would be the depth direction, the direction away from the camera. Do you have any reference points for that direction? It looks to me as though you might be able to use one complete tile on the left wall, before the window starts. But depending on how the corner between the two walls is tiled, that might be slightly off.
To illustrate these ideas, look at the picture above. Since the red lines appear almost horizontal, seeing the effects of perspective there is pretty hard. Therefore I'll do the other direction. Suppose the tile in the corner is indeed the same visible size as all the other tiles on the wall. So you know the real world distance between A1 and B1. You project along the blue vertical lines (vertical in the real world, not neccessarily the image) down to A2 and B2 which is where the left wall plane meets the floor plane.
Why do they meet there? Well, the lines A1,A2 is where the left all meets the back wall. The line A2,A3 is where the back wall meets the floor. Both of these plane intersections are actually visible at least in part, which made drawing the lines possible. So at A2 all three planes meet, and connecting that to the far point F gives the third edge, where the left wall meets the floor.
Since the segments A1,B1 and A2,B2 are just vertically transported versions of one another in the real world, they have equals length. That transportation was along the left wall in the vertical direction. Now transport them again, this time in the floor plane and in the left-right direction. You do so using the red lines, which are either parallel or meet at a point (which is pretty far away in this example). These red lines A2,A3 and B2,B3 are parallel in the real world, and their distance is still the edge length of that tile.
Now start measuring something, e.g. distance between C and D. To do that, compute the cross ratio (F,A3;B3,C) which expresses the distance from A3 to C, expressed in multiples of the distance from A3 to B3, and using F as the point at infinity. Do the same for D, and then the difference will be the length from C to D, expressed in multiples of the distance from A3 to B3. So the distance between C and D is 4.42 tile edge lengths in this example. Scale your image to fit this figure.