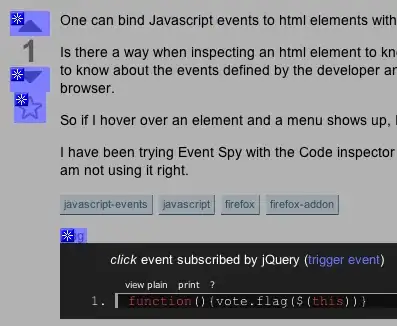
I had the same question. I could not find a clear direct answer by searching online, but after running some tests I have an idea what cv2.getOptimalNewCameraMatrix function actually does for the user.
I used the same images mentioned in openCV calibration tutorial (you can find the images in here named left01.jpg to left14.jpg (Actually left10.jpg seems to be missing but that's fine)) After the calibration steps -assuming the square sizes are 30 mm- in the tutorial I got this camera matrix:
mtx = [[534.07088364 0. 341.53407554]
[ 0. 534.11914595 232.94565259]
[ 0. 0. 1. ]]
The new camera matrix obtained, on the other hand, using the command newcameramtx, roi = cv2.getOptimalNewCameraMatrix(mtx, dist, (w,h), 1, (w,h)) is
newcameramtx = [[457.92434692 0. 342.55548195]
[ 0. 456.2421875 233.34661351]
[ 0. 0. 1. ]]
Notice that here alpha=1, but it could have been another value between [0,1]. Using another value would give a different newcameramtx.
So far nothing is new. Then, I "undistorted" all the used images during the calibration and saved them into two new folders. One folder (Let's call it the 1st folder) is filled with the undistorted images directly using the obtained intrinsic camera (ie. mtx) and distortion coefficients (dist), and the other one (Let's call it the 2nd folder) is filled with the undistorted images using the newcameramtx and the same distortion coefficients (dist). To be explicit, I used the commands cv2.undistort(img, mtx, dist, None, mtx) and cv2.undistort(img, mtx, dist, None, newcameramtx) respectively and saved the result images into the mentioned two folders. I did NOT cropped the undistorted images using the roi before saving. The result images are just like you have found and gave in the question.
Then, using the undistorted images in the 1st folder, I re-executed the calibration process and I found the following camera matrices:
mtx_1stFolder = [[533.72669262 0. 341.96641109]
[ 0. 533.73880924 232.9742336 ]
[ 0. 0. 1. ]]
newcameramtx_1stFolder = [[533.41644287 0. 341.35446736]
[ 0. 532.47808838 232.56343633]
[ 0. 0. 1. ]]
Doing the same for the 2nd folder gave the following camera matrices:
mtx_2ndFolder = [[458.04299944 0. 342.94915275]
[ 0. 456.31672142 233.39481945]
[ 0. 0. 1. ]]
newcameramtx_2ndFolder = [[458.24960327 0. 342.20507346]
[ 0. 455.25088501 232.99452259]
[ 0. 0. 1. ]]
Now, notice here how close mtx, mtx_1stFolder, and newcameramtx_1stFolder to each other. And similarly notice how close newcameramtx, mtx_2ndFolder, and newcameramtx_2ndFolder to each other as well.
Based on these observations my idea is that undistorting the images directly using the obtained intrinsic camera and distortion coefficients does not affect the camera matrix and it returns the same size images accordingly, but these resulting images loses some pixels. If you are fine with that loss, you are safe to not to use cv2.getOptimalNewCameraMatrix at all. If you need, however, the information given in the lost pixels, you also have an option to undistort your images accordingly setting up an alpha parameter between [0,1] into the same image size or any size you desire. This operation, however, would definitely destroy your camera matrix and you would need a new calibration upon the new undistorted images. cv2.getOptimalNewCameraMatrix function gives an estimation of what would be the new camera matrix without having you to require to do a new calibration. This explains why newcameramtx and mtx_2ndFolder are very close to each other.
This also seems to be explaining why mtx_2ndFolder and newcameramtx_2ndFolder are close to each other, because there is not much left to undistort.(And similarly for mtx_1stFolder and newcameramtx_1stFolder)
One thing I have not mentioned so far is the distortion coefficients(dist) for each calibration processes. This actually keeps me away from saying my idea is for sure, so I am all open to corrections on my idea. Intuitively, I am expecting some distortion coefficients for the first calibration since the images are obviously distorted. As expected, the distortion coefficient vector is found as:
dist = [[-0.29297164 0.10770696 0.00131038 -0.0000311 0.0434798 ]]
On the other hand, I was expecting that the calibration on the undistorted images would give less coefficients, ideally 0 since the all distortions are ideally removed. However,
Calibration on the 1st folder gives:
dist = [[ 0.00760897 -0.07313015 0.0002162 0.0003522 0.1605208 ]]
Calibration on the 2nd folder gives:
dist = [[ 0.00135068 -0.02390678 0.0001996 0.0003413 0.0580141 ]]
For the first three terms, the results are as in the expectation way becoming less in the magnitude towards zero, however they are not drastically closer to 0. Also for the last two terms the coefficients are increased which is the opposite of my expectation. If anyone have an idea why this is the case I would highly appreciate.