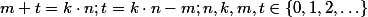From several posts inside stackoverflow and outside, I have come to know how to detect cycles in a linked list, the length of a cycle. I also found the method on how to detect the start of the loop.
Here are the steps again for reference.
Detecting Loop:
Have two pointers, classically called hare and tortoise. Move hare by 2 steps and tortoise by 1. If they meet at some point, then there is surely a cycle and the meeting point is obviously inside the cycle.
Finding length of Loop:
Keep one pointer fixed at meeting point while increment the other until they are same again. Increment a counter as you go along and the counter value at meet will be the length of cycle.
Find the start of cycle
Take one pointer to start of the list and keep the other at the meeting point. Now increment both by one and the meet point is the start of loop. I verified the method using some cases on paper, but I don't understand why it should work.
Can someone, provide a mathematical proof as to why this method works?

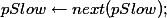
 , then STOP as a loop has just been found.
, then STOP as a loop has just been found.
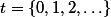
 and
and  ), and setting t=0 as iteration value when
), and setting t=0 as iteration value when 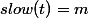 then:
then:
 .
.
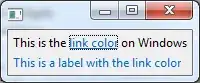 which generates values of t that are valid solutions to the equation described above:
which generates values of t that are valid solutions to the equation described above: