What you're doing seems a bit weird to me, at least you seem to use a single set of y values to do the interpolation. What I suggest is not performing two interpolations one after the other, but considering your y(z,x) function as the result of a pure 2d interpolation problem.
So as I noted in a comment, I suggest using scipy.interpolate.LinearNDInterpolator, the same object that griddata uses under the hood for bilinear interpolatin. As we've also discussed in comments, you need to have a single interpolator that you can query multiple times afterwards, so we have to use the lower-level interpolator object, as that is callable.
Here's a full example of what I mean, complete with dummy data and plotting:
import numpy as np
import scipy.interpolate as interp
import matplotlib.pyplot as plt
# create dummy data
zlist = range(4) # z values
# one pair of arrays for each z value in a list:
xlist = [np.linspace(-1,1,41),
np.linspace(-1,1,61),
np.linspace(-1,1,55),
np.linspace(-1,1,51)]
funlist = [lambda x:0.1*np.ones_like(x),
lambda x:0.2*np.cos(np.pi*x)+0.4,
lambda x:np.exp(-2*x**2)+0.5,
lambda x:-0.7*np.abs(x)+1.7]
ylist = [f(x) for f,x in zip(funlist,xlist)]
# create contiguous 1d arrays for interpolation
all_x = np.concatenate(xlist)
all_y = np.concatenate(ylist)
all_z = np.concatenate([np.ones_like(x)*z for x,z in zip(xlist,zlist)])
# create a single linear interpolator object
yfun = interp.LinearNDInterpolator((all_z,all_x),all_y)
# generate three interpolated sets: one with z=2 to reproduce existing data,
# two with z=1.5 and z=2.5 respectively to see what happens
xplot = np.linspace(-1,1,30)
z = 2
y_repro = yfun(z,xplot)
z = 1.5
y_interp1 = yfun(z,xplot)
z = 2.5
y_interp2 = yfun(z,xplot)
# plot the raw data (markers) and the two interpolators (lines)
fig,ax = plt.subplots()
for x,y,z,mark in zip(xlist,ylist,zlist,['s','o','v','<','^','*']):
ax.plot(x,y,'--',marker=mark,label='z={}'.format(z))
ax.plot(xplot,y_repro,'-',label='z=2 interp')
ax.plot(xplot,y_interp1,'-',label='z=1.5 interp')
ax.plot(xplot,y_interp2,'-',label='z=2.5 interp')
ax.set_xlabel('x')
ax.set_ylabel('y')
# reduce plot size and put legend outside for prettiness, see also http://stackoverflow.com/a/4701285/5067311
box = ax.get_position()
ax.set_position([box.x0, box.y0, box.width * 0.8, box.height])
ax.legend(loc='center left', bbox_to_anchor=(1, 0.5))
plt.show()
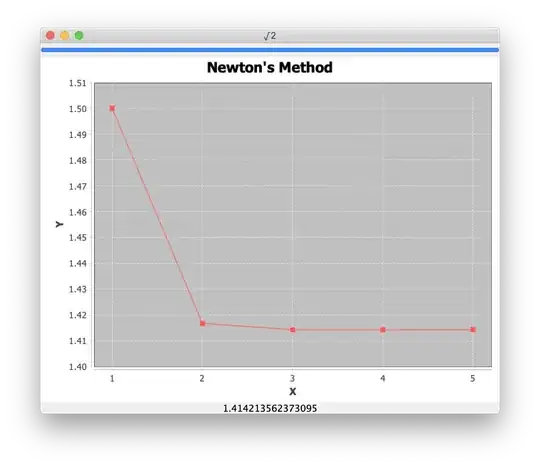
You didn't specify how you series of (x,y) array pairs are stored, I used a list of numpy ndarrays. As you see, I flattened the list of 1d arrays into a single set of 1d arrays: all_x, all_y, all_z. These can be used as scattered y(z,x) data from which you can construct the interpolator object. As you can see in the result, for z=2 it reproduces the input points, and for non-integer z it interpolates between the relevant y(x) curves.
This method should be applicable to your dataset. One note, however: you have huge numbers on a logarithmic scale on your x axis. This alone could lead to numeric instabilities. I suggest that you also try performing the interpolation using log(x), it might behave better (this is just a vague guess).