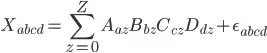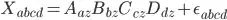I am trying to decompose a 3D matrix using python library scikit-tensor. I managed to decompose my Tensor (with dimensions 100x50x5) into three matrices. My question is how can I compose the initial matrix again using the decomposed matrix produced with Tensor factorization? I want to check if the decomposition has any meaning. My code is the following:
import logging
from scipy.io.matlab import loadmat
from sktensor import dtensor, cp_als
import numpy as np
//Set logging to DEBUG to see CP-ALS information
logging.basicConfig(level=logging.DEBUG)
T = np.ones((400, 50))
T = dtensor(T)
P, fit, itr, exectimes = cp_als(T, 10, init='random')
// how can I re-compose the Matrix T? TA = np.dot(P.U[0], P.U[1].T)
I am using the canonical decomposition as provided from the scikit-tensor library function cp_als. Also what is the expected dimensionality of the decomposed matrices?