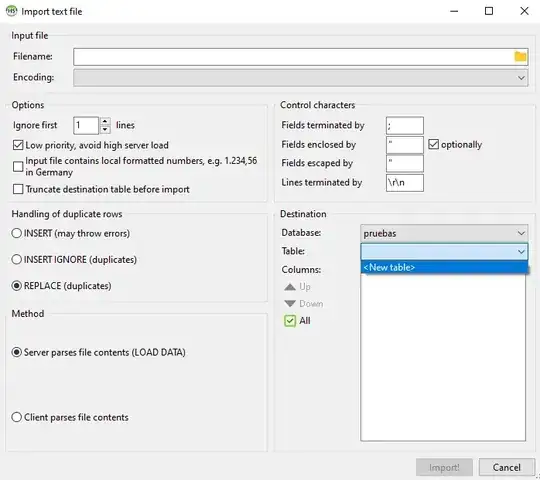
n.m. answered the question as I asked and pictured it, but upon programming I soon noticed that there was a common case where all vertices would be "outside" vertices (this can be easily seen on triangles, and can occur for other polygons too).
The text explanation.
The solution I used was to look at the normal vectors of the edges leading into and exiting each vertex. The vertices we want to extend are vertices that have at least one edge normal with a minimum angle of less than 90 degrees to the delta vector we are extending by.
The outward-facing edge normals on a counterclockwise-wound polygon can be found by:
normal = (currentVertex.y - nextVertex.y, nextVertex.x - currentVertex.x)
Note that since we don't care about the exact angle, we don't need to normalize (make a unit vector of) the normal, which saves a square root.
To compare it to the delta vector, we use the dot product:
dot = edgeNormal.dot(deltaVector)
If the result is greater than zero, the minimum angle is acute (less than 90). If the result is exactly zero, the vectors are perpendicular. If the result is less than zero, the minimum angle is obtuse. It is worth noting when the vectors are perpendicular, since it lets us avoid adding extra vertices to the extended polygon.
If you want to visualize how the angle works with the dot product, like I did, just look at a graph of arc cosine (normally you get the angle via acos(dot)).
Now we can find the vertices that have one acute and one not-acute minimum angle between its edge normals and the delta vector. Everything on the "acute side" of these vertices has the delta vector added to it, and everything on the "obtuse side" stays the same. The two boarder vertices themselves are duplicated, having one extended and one staying the same, unless the "obtuse side" is exactly perpendicular to the delta vector (in this case we only need to extend the vertex, since otherwise we would have two vertices on the same line).
Here is the C++ code for this solution.
It may look a little long, but it is actually quite straightforward and has many comments so it hopefully shouldn't be hard to follow.
It is part of my Polygon class, which has a std::vector of counterclockwise-wound vertices. units::Coordinate are floats, and units::Coordinate2D is a vector class that I feel should be self-explanatory.
// Compute the normal of an edge of a polygon with counterclockwise winding, without normalizing it to a unit vector.
inline units::Coordinate2D _get_non_normalized_normal(units::Coordinate2D first, units::Coordinate2D second) {
return units::Coordinate2D(first.y - second.y, second.x - first.x);
}
enum AngleResult {
ACUTE,
PERPENDICULAR,
OBTUSE
};
// Avoid accumulative floating point errors.
// Choosing a good epsilon is extra important, since we don't normalize our vectors (so it is scale dependent).
const units::Coordinate eps = 0.001;
// Check what kind of angle the minimum angle between two vectors is.
inline AngleResult _check_min_angle(units::Coordinate2D vec1, units::Coordinate2D vec2) {
const units::Coordinate dot = vec1.dot(vec2);
if (std::abs(dot) <= eps)
return PERPENDICULAR;
if ((dot + eps) > 0)
return ACUTE;
return OBTUSE;
}
Polygon Polygon::extend(units::Coordinate2D delta) const {
if (delta.isZero()) { // Isn't being moved. Just return the current polygon.
return Polygon(*this);
}
const std::size_t numVerts = vertices_.size();
if (numVerts < 3) {
std::cerr << "Error: Cannot extend polygon (polygon invalid; must have at least three vertices).\n";
return Polygon();
}
// We are interested in extending from vertices that have at least one edge normal with a minimum angle acute to the delta.
// With a convex polygon, there will form a single contiguous range of such vertices.
// The first and last vertex in that range may need to be duplicated, and then the vertices within the range
// are projected along the delta to form the new polygon.
// The first and last vertices are defined by the vertices that have only one acute edge normal.
// Whether the minimum angle of the normal of the edge made from the last and first vertices is acute with delta.
const AngleResult firstEdge = _check_min_angle(_get_non_normalized_normal(vertices_[numVerts-1], vertices_[0]), delta);
const bool isFirstEdgeAcute = firstEdge == ACUTE;
AngleResult prevEdge = firstEdge;
AngleResult currEdge;
bool found = false;
std::size_t vertexInRegion;
for (std::size_t i = 0; i < numVerts - 1; ++i) {
currEdge = _check_min_angle(_get_non_normalized_normal(vertices_[i], vertices_[i+1]), delta);
if (isFirstEdgeAcute != (currEdge == ACUTE)) {
// Either crossed from inside to outside the region, or vice versa.
// (One side of the vertex has an edge normal that is acute, the other side obtuse.)
found = true;
vertexInRegion = i;
break;
}
prevEdge = currEdge;
}
if (!found) {
// A valid polygon has two points that define where the region starts and ends.
// If we didn't find one in the loop, the polygon is invalid.
std::cerr << "Error: Polygon can not be extended (invalid polygon).\n";
return Polygon();
}
found = false;
std::size_t first, last;
// If an edge being extended is perpendicular to the delta, there is no need to duplicate that vertex.
bool shouldDuplicateFirst, shouldDuplicateLast;
// We found either the first or last vertex for the region.
if (isFirstEdgeAcute) {
// It is the last vertex in the region.
last = vertexInRegion;
shouldDuplicateLast = currEdge != PERPENDICULAR; // currEdge is either perpendicular or obtuse.
// Loop backwards from the end to find the first vertex.
for (std::size_t i = numVerts - 1; i > 0; --i) {
currEdge = _check_min_angle(_get_non_normalized_normal(vertices_[i-1], vertices_[i]), delta);
if (currEdge != ACUTE) {
first = i;
shouldDuplicateFirst = currEdge != PERPENDICULAR;
found = true;
break;
}
}
if (!found) {
std::cerr << "Error: Polygon can not be extended (invalid polygon).\n";
return Polygon();
}
} else {
// It is the first vertex in the region.
first = vertexInRegion;
shouldDuplicateFirst = prevEdge != PERPENDICULAR; // prevEdge is either perpendicular or obtuse.
// Loop forwards from the first vertex to find where it ends.
for (std::size_t i = vertexInRegion + 1; i < numVerts - 1; ++i) {
currEdge = _check_min_angle(_get_non_normalized_normal(vertices_[i], vertices_[i+1]), delta);
if (currEdge != ACUTE) {
last = i;
shouldDuplicateLast = currEdge != PERPENDICULAR;
found = true;
break;
}
}
if (!found) {
// The edge normal between the last and first vertex is the only non-acute edge normal.
last = numVerts - 1;
shouldDuplicateLast = firstEdge != PERPENDICULAR;
}
}
// Create the new polygon.
std::vector<units::Coordinate2D> newVertices;
newVertices.reserve(numVerts + (shouldDuplicateFirst ? 1 : 0) + (shouldDuplicateLast ? 1 : 0) );
for (std::size_t i = 0; i < numVerts; ++i) {
// Extend vertices in the region first-to-last inclusive. Duplicate first/last vertices if required.
if (i == first && shouldDuplicateFirst) {
newVertices.push_back(vertices_[i]);
newVertices.push_back(vertices_[i] + delta);
} else if (i == last && shouldDuplicateLast) {
newVertices.push_back(vertices_[i] + delta);
newVertices.push_back(vertices_[i]);
} else {
newVertices.push_back( isFirstEdgeAcute ? // Determine which range to use.
( (i <= last || i >= first) ? vertices_[i] + delta : vertices_[i] ) : // Range overlaps start/end of the array.
( (i <= last && i >= first) ? vertices_[i] + delta : vertices_[i] )); // Range is somewhere in the middle of the array.
}
}
return Polygon(newVertices);
}
So far I tested this code with triangles, rectangles, approximated circles, and arbitrary convex polygons made by extending the approximated circles sequentially by many different delta vectors.
Please note that this solution is still only valid for convex polygons.