What is fuzzy logic?

Question

I'm working with a couple of AI algorithms at school and I find people use the words Fuzzy Logic to explain any situation that they can solve with a couple of cases. When I go back to the books I just read about how instead of a state going from On to Off it's a diagonal line and something can be in both states but in different "levels".

I've read the wikipedia entry and a couple of tutorials and even programmed stuff that "uses fuzzy logic" (an edge detector and a 1-wheel self-controlled robot) and still I find it very confusing going from Theory to Code... for you, in the less complicated definition, what is fuzzy logic?

Answer 1

Fuzzy logic is logic where state membership is, essentially, a float with range 0..1 instead of an int 0 or 1. The mileage you get out of it is that things like, for example, the changes you make in a control system are somewhat naturally more fine-tuned than what you'd get with naive binary logic.

An example might be logic that throttles back system activity based on active TCP connections. Say you define "a little bit too many" TCP connections on your machine as 1000 and "a lot too many" as 2000. At any given time, your system has a "too many TCP connections" state from 0 (<= 1000) to 1 (>= 2000), which you can use as a coefficient in applying whatever throttling mechanisms you have available. This is much more forgiving and responsive to system behavior than naive binary logic that only knows how to determine "too many", and throttle completely, or "not too many", and not throttle at all.

Answer 2

I'd like to add to the answers (that have been modded up) that, a good way to visualize fuzzy logic is follows:

Traditionally, with binary logic you would have a graph whose membership function is true or false whereas in a fuzzy logic system, the membership function is not.

1|
 |   /\
 |  /  \
 | /    \
0|/      \
 ------------
   a  b c   d

Assume for a second that the function is "likes peanuts"

a. kinda likes peanuts
b. really likes peanuts
c. kinda likes peanuts
d. doesn't like peanuts

The function itself doesn't have to be triangular and often isn't (it's just easier with ascii art).

A fuzzy system will likely have many of these, some even overlapping (even opposites) like so:

1|   A    B
 |   /\  /\      A = Likes Peanuts
 |  /  \/  \     B = Doesn't Like Peanuts
 | /   /\   \
0|/   /  \   \
 ------------
  a  b  c d

so now c is "kind likes peanuts, kinda doesn't like peanuts" and d is "really doesn't like peanuts"

And you can program accordingly based on that info.

Hope this helps for the visual learners out there.

Answer 3

The best definition of fuzzy logic is given by its inventor Lotfi Zadeh:

“Fuzzy logic means of representing problems to computers in a way akin to the way human solve them and the essence of fuzzy logic is that everything is a matter of degree.”

The meaning of solving problems with computers akin to the way human solve can easily be explained with a simple example from a basketball game; if a player wants to guard another player firstly he should consider how tall he is and how his playing skills are. Simply if the player that he wants to guard is tall and plays very slow relative to him then he will use his instinct to determine to consider if he should guard that player as there is an uncertainty for him. In this example the important point is the properties are relative to the player and there is a degree for the height and playing skill for the rival player. Fuzzy logic provides a deterministic way for this uncertain situation.

There are some steps to process the fuzzy logic (Figure-1). These steps are; firstly fuzzification where crisp inputs get converted to fuzzy inputs secondly these inputs get processed with fuzzy rules to create fuzzy output and lastly defuzzification which results with degree of result as in fuzzy logic there can be more than one result with different degrees.

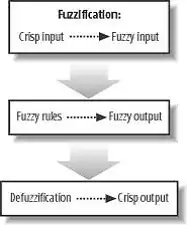
Figure 1 – Fuzzy Process Steps (David M. Bourg P.192)

To exemplify the fuzzy process steps, the previous basketball game situation could be used. As mentioned in the example the rival player is tall with 1.87 meters which is quite tall relative to our player and can dribble with 3 m/s which is slow relative to our player. Addition to these data some rules are needed to consider which are called fuzzy rules such as;

if player is short but not fast then guard,
if player is fast but not short then don’t guard
If player is tall then don’t guard
If player is average tall and average fast guard

Figure 2 – how tall

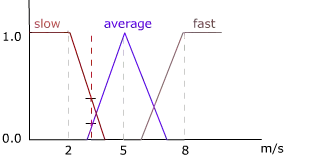
Figure 3- how fast

According to the rules and the input data an output will be created by fuzzy system such as; the degree for guard is 0.7, degree for sometimes guard is 0.4 and never guard is 0.2.

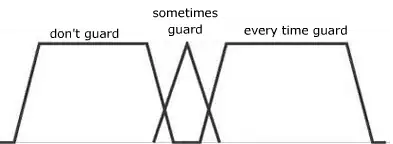
Figure 4-output fuzzy sets

On the last step, defuzzication, is using for creating a crisp output which is a number which may determine the energy that we should use to guard the player during game. The centre of mass is a common method to create the output. On this phase the weights to calculate the mean point is totally depends on the implementation. On this application it is considered to give high weight to guard or not guard but low weight given to sometimes guard. (David M. Bourg, 2004)

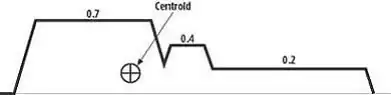
Figure 5- fuzzy output (David M. Bourg P.204)

  Output = [0.7 * (-10) + 0.4 * 1 + 0.2 * 10] / (0.7 + 0.4 + 0.2) ≈ -3.5

As a result fuzzy logic is using under uncertainty to make a decision and to find out the degree of decision. The problem of fuzzy logic is as the number of inputs increase the number of rules increase exponential.

For more information and its possible application in a game I wrote a little article check this out

Answer 4

To build off of chaos' answer, a formal logic is nothing but an inductively defined set that maps sentences to a valuation. At least, that's how a model theorist thinks of logic. In the case of a sentential boolean logic:

 (basis clause) For all A, v(A) in {0,1}
 (iterative) For the following connectives,
   v(!A) = 1 - v(A)
   v(A & B) = min{v(A), v(B)}
   v(A | B) = max{v(A), v(B)}
 (closure) All sentences in a boolean sentential logic are evaluated per above.

A fuzzy logic changes would be inductively defined:

 (basis clause) For all A, v(A) between [0,1]
 (iterative) For the following connectives,
   v(!A) = 1 - v(A)
   v(A & B) = min{v(A), v(B)}
   v(A | B) = max{v(A), v(B)}
 (closure) All sentences in a fuzzy sentential logic are evaluated per above.

Notice the only difference in the underlying logic is the permission to evaluate a sentence as having the "truth value" of 0.5. An important question for a fuzzy logic model is the threshold that counts for truth satisfaction. This is to ask: for a valuation v(A), for what value D it is the case the v(A) > D means that A is satisfied.

If you really want to found out more about non-classical logics like fuzzy logic, I would recommend either An Introduction to Non-Classical Logic: From If to Is or Possibilities and Paradox

Putting my coder hat back on, I would be careful with the use of fuzzy logic in real world programming, because of the tendency for a fuzzy logic to be undecidable. Maybe it's too much complexity for little gain. For instance a supervaluational logic may do just fine to help a program model vagueness. Or maybe probability would be good enough. In short, I need to be convinced that the domain model dovetails with a fuzzy logic.

Answer 5

Maybe an example clears up what the benefits can be:

Let's say you want to make a thermostat and you want it to be 24 degrees.

---

This is how you'd implement it using boolean logic:

• Rule1: heat up at full power when it's colder than 21 degrees.
• Rule2: cool down at full power when it's warmer than 27 degrees.

Such a system will only once and a while be 24 degrees, and it will be very inefficient.

---

Now, using fuzzy logic, it would be like something like this:

• Rule1: For each degree that it's colder than 24 degrees, turn up the heater one notch (0 at 24).
• Rule2: For each degree that it's warmer than 24 degress, turn up the cooler one notch (0 at 24).

This system will always be somewhere around 24 degrees, and it only once and will only once and a while make a tiny adjustment. It will also be more energy-efficient.

Answer 6

Well, you could read the works of Bart Kosko, one of the 'founding fathers'. 'Fuzzy Thinking: The New Science of Fuzzy Logic' from 1994 is readable (and available quite cheaply secondhand via Amazon). Apparently, he has a newer book 'Noise' from 2006 which is also quite approachable.

Basically though (in my paraphrase - not having read the first of those books for several years now), fuzzy logic is about how to deal with the world where something is perhaps 10% cool, 50% warm, and 10% hot, where different decisions may be made on the degree to which the different states are true (and no, it wasn't entirely an accident that those percentages don't add up to 100% - though I'd accept correction if needed).

Answer 7

A very good explanation, with a help of Fuzzy Logic Washing Machines.

Answer 8

I know what you mean about it being difficult to go from concept to code. I'm writing a scoring system that looks at the values of sysinfo and /proc on Linux systems and comes up with a number between 0 and 10, 10 being the absolute worst. A simple example:

You have 3 load averages (1, 5, 15 minute) with (at least) three possible states, good, getting bad, bad. Expanding that, you could have six possible states per average, adding 'about to' to the three that I just noted. Yet, the result of all 18 possibilities can only deduct 1 from the score. Repeat that with swap consumed, actual VM allocated (committed) memory and other stuff .. and you have one big bowl of conditional spaghetti :)

Its as much a definition as it is an art, how you implement the decision making process is always more interesting than the paradigm itself .. whereas in a boolean world, its rather cut and dry.

It would be very easy for me to say if load1 < 2 deduct 1, but not very accurate at all.

If you can teach a program to do what you would do when evaluating some set of circumstances and keep the code readable, you have implemented a good example of fuzzy logic.

Answer 9

Fuzzy Logic is a problem-solving methodology that lends itself to implementation in systems ranging from simple, small, embedded micro-controllers to large, networked, multi-channel PC or workstation-based data acquisition and control systems. It can be implemented in hardware, software, or a combination of both. Fuzzy Logic provides a simple way to arrive at a definite conclusion based upon vague, ambiguous, imprecise, noisy, or missing input information. Fuzzy Logic approach to control problems mimics how a person would make decisions, only much faster.

Fuzzy logic has proved to be particularly useful in expert system and other artificial intelligence applications. It is also used in some spell checkers to suggest a list of probable words to replace a misspelled one.

To learn more, just check out: http://en.wikipedia.org/wiki/Fuzzy_logic.

Answer 10

Fuzzy logic is calculating algorithm based on human like way of thinking. It is particularly useful when there is a large number of input variables. One online fuzzy logic calculator for two variables input is given:

http://www.cirvirlab.com/simulation/fuzzy_logic_calculator.php

Answer 11

The following is sort of an empirical answer.

A simple (possibly simplistic answer) is that "fuzzy logic" is any logic that returns values other than straight true / false, or 1 / 0. There are a lot of variations on this and they tend to be highly domain specific.

For example, in my previous life I did search engines that used "content similarity searching" as opposed to then common "boolean search". Our similarity system used the Cosine Coefficient of weighted-attribute vectors representing the query and the documents and produced values in the range 0..1. Users would supply "relevance feedback" which was used to shift the query vector in the direction of desirable documents. This is somewhat related to the training done in certain AI systems where the logic gets "rewarded" or "punished" for results of trial runs.

Right now Netflix is running a competition to find a better suggestion algorithm for their company. See http://www.netflixprize.com/. Effectively all of the algorithms could be characterized as "fuzzy logic"