As underlined by Spektre, the actual FLOPS (Floating Point OPerations per Second) depend on the particular hardware and implementation and higher FLOP (Floating Point OPeration) algorithms may correspond to lower FLOPS implementations, just because with such implementations you can more effectively exploit the hardware.
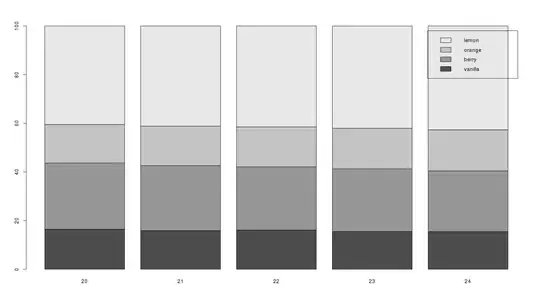
If you want to compute the number of floating point operations for a Decimation In Time radix-2 approach, the you can refer to the following figure:
Let N the length of the sequence to be transformed. There is an overall number of log2N stages and each stage contains N/2 butterflies. Let us then consider the generic butterfly:
Let us rewrite the output of the generic butterfly as
E(i + 1) = E(i) + W * O(i)
O(i + 1) = E(i) - W * O(i)
A butterfly thus involves one complex multiplication and two complex additions. On rewriting the above equations in terms of real and imaginary parts, we have
real(E(i + 1)) = real(E(i)) + (real(W) * real(O(i)) - imag(W) * imag(O(i)))
imag(E(i + 1)) = imag(E(i)) + (real(W) * imag(O(i)) + imag(W) * real(O(i)))
real(O(i + 1)) = real(O(i)) - (real(W) * real(O(i)) - imag(W) * imag(O(i)))
imag(O(i + 1)) = imag(O(i)) - (real(W) * imag(O(i)) + imag(W) * real(O(i)))
Accordingly, we have
4 multiplications
real(W) * real(O(i)),
imag(W) * imag(O(i)),
real(W) * imag(O(i)),
imag(W) * real(O(i)).
6 sums
real(W) * real(O(i)) – imag(W) * imag(O(i)) (1)
real(W) * imag(O(i)) + imag(W) * real(O(i)) (2)
real(E(i)) + eqn.1
imag(E(i)) + eqn.2
real(E(i)) – eqn.1
imag(E(i)) – eqn.2
Therefore, the number of operations for the Decimation In Time radix 2 approach are
2N * log2(N) multiplications
3N * log2(N) additions
These operation counts may change if the multiplications are differently arranged, see Complex numbers product using only three multiplications.
The same results apply to the case of Decimation in Frequency radix 2, see figure